Abstract—Kalman filters have received much attention with the increasing demands for robotic automation. This paper briefly surveys the recent developments for robot vision. Among many factors that affect the performance of a robotic system, Kalman filters have made great contributions to vision perception. Kalman filters solve uncertainties in robot localization, navigation, following, tracking, motion control, estimation and prediction, visual servoing and manipulation, as well as structure reconstruction from a sequence of images. In the 50^th anniversary, we have noticed that more than 20 kinds of Kalman filters have been developed so far. These include extended Kalman filters and unscented Kalman filters. In the last 30 years, about 800 publications have reported the capability of these filters in solving robot vision problems. Such problems encompass a rather wide application area, such as object modeling, robot control, target tracking, surveillance, search, recognition, and assembly, as well as robotic manipulation, localization, mapping, navigation, and exploration. These reports are summarized in this review to enable easy referral to suitable methods for practical solutions. Representative contributions and future research trends are also addressed in an abstract level.

 

Index Terms—Computer vision, estimation, Kalman Filter, localization, prediction, robot vision, particle filter.

 

I.    INTRODUCTION

Kalman filters have become a standard approach for reducing errors in a least-squares sense and in using measurements from different sources. Among its many applications, the Kalman filter is most essentially a part of vision development in robots. The purpose of the filter is to use visual measurements that contain noises and uncertainties captured by video cameras over time. Using a Kalman filter can produce values that tend to be closer to the true spatial measurements of the robots and targets, i.e., robot self-localization [1] and object estimation [2].

Localization by artificial vision is a key issue for a mobile robot, particularly in environments where accurate global positioning systems (GPS) and inertial sensors are not available. In these environments, accurate and efficient robot localization is not a trivial task, because increased accuracy usually leads to decreased efficiency, and vice versa [3]. Automatic detection and tracking are also interesting areas of research on related applications such as missile tracking and security systems, as well as commercial fields like virtual reality interfaces, robot vision, etc. In vision-aided navigation that enables precision landing, Kalman filters can tightly integrate visual feature observations with other measurements from GPS, inertial, or force sensors. The filter accurately estimates the terrain-relative position and velocity in a resource-adaptive and real-time fashion [4-6].

Pose estimation from visual sensors is widely practiced in robotic applications. This estimation can be made from the homographies of different coordinates and from the projection geometry of the vision cameras. Measurement integration from multiple sensors is becoming more attractive because of its robustness and flexibility [7]. For an autonomous robot to capture non-cooperative targets, its vision system needs to employ an algorithm from a Kalman filter for detecting the target, determining the quality of the lock, and predicting the motion [8]. For robust visual tracking control, a Kalman filter can be used to estimate interesting parameters and overcome the temporary occlusion problem [9]. For such functions, the unscented Kalman filter (UKF) is used to fuse information from different sensors.

Three-dimensional (3D) reconstruction from 2D images is the foundation for solving the problems in robotics and computer vision. One of the main problems in vision-based unmanned vehicles is localizing the mobile robot in an indoor, outdoor, or unstructured environment by classifying, segmenting, and recognizing the environment. One of the most active topics in robotics today is simultaneous localization and mapping (SLAM) [10], where the extended Kalman filter (EKF) is often necessary for robot navigation. EKF is the nonlinear version of the Kalman filter. However, because of the high computational complexity, it has strict limits on the number and stability of feature points. In contrast, the traditional method selects a few corners or straight lines as feature points [11], where the scale-invariant feature transform (SIFT) can improve the convergence velocity. Today, Kalman filters play roles in most autonomous robotic systems.

The scope of this paper is restricted to Kalman filters in the field of robot vision. Although this topic has attracted researchers as early as since the 1980s [12], this survey concentrates on the contributions of the last 5 years. No review of this nature can possibly cite each and every paper that has been published. Therefore, we include only what we believe to be representative samples of important works and broad trends from recent years. In many cases, references were provided to better summarize and draw distinctions among key ideas and approaches.

The paper has six more sections. Section II briefly provides an overview of related contributions. Section III introduces the typical formulation of KF and EKF for robot vision. Section IV lists the relevant tasks, problems, and applications of Kalman filters. Section V concentrates on how to solve such problems using KF. We show the available methods and solutions to specific tasks. Section VI is a discussion of our impressions on current and future trends. Section VII is the conclusion.

II.   Overview of Contributions

A.  Summary

From 1980 to 2010, about 800 research papers with topics on or closely related to, Kalman filters for robot vision were published. Fig. 1 shows the yearly distribution of these published papers. The number of records for 2010 is not complete because only the publications in the first two quarters of 2010 were searched, and most articles have not yet been included in the indexing databases. The plot shows that the topic of Kalman filters: (1) emerged around the year 1983 and developed within the first 10 years; (2) warmed up within the following 10 years; (3) rapidly developed within the next 10 years; and (4) reached peak activity within the past five years.

 

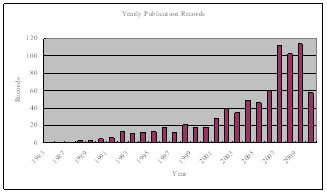
Fig. 1. Yearly published records from 1983 to 2010.

 

B.  Representatives

Kalman filters have many applications in robotic vision perception. Their most significant roles are summarized in the following list:

(1)     Robot control [13];

(2)     Object tracking [14];

(3)     Path following [15];

(4)     Data estimation and prediction [16;17];

(5)     Robot localization [3;18];

(6)     Robotic manipulation [19];

(7)     SLAM [11;20;21];

(8)     3D Modeling [22];

(9)     Visual servoing [23;24];

(10)  Visual navigation [4;25]; and

(11)  Leader-follower system [26].

 

The commonly used methods for solving robotic vision problems are listed below:

(1)     Kalman filter [27];

(2)     Self-tuning Kalman filter [28];

(3)     Steady-state Kalman filter [29];

(4)     Ensemble Kalman filter (EnKF) [30;31];

(5)     Adaptive Kalman filter (AKF) [32];

(6)     Switching Kalman filter (SKF) [32];

(7)     Fuzzy Kalman Filter (FKF) [33];

(8)     Extended Kalman filter (EKF) [34];

(9)     Motor EKF (MEKF) [35];

(10)  Hybrid EKF (HEKF) [36];

(11)  Augmented state EKF [37];

(12)  Modified covariance EKF (MV-EKF) [38];

(13)  Iterative Adaptive EKF (IA-EKF) [24];

(14)  Unscented Kalman filter (UKF) [39];

(15)  Dual UKF (DUKF) [40];

(16)  Recursive UKF [41];

(17)  Square root UKF (SR-UKF) [42];

(18)  Kinematic Kalman filter (KKF) [43];

(19)  Multidimensional kinematic Kalman filter (MD-KKF) [43];

(20)  Fuzzy logic controller Kalman filter (FLC-KF) [44];

(21)  Neural Network aided EKF (NN-EKF) [45]; and

(22)  Particle swarm optimization aided EKF (PSO-EKF) [46].

 

Among the variety of developed filters, the main differences and remarkable features can be summarized briefly. EKF is the nonlinear version of KF which linearizes about the current mean and covariance [47]. UKF uses the unscented transform to pick a minimal set of sample points around the mean so that the filters can avoid poor performance when the state transition and observation models are highly non-linear. EnKF is a recursive filter suitable for problems with a large number of variables, such as discretizations of partial differential equations in geophysical models [30;31]. It is an important data assimilation component of ensemble forecasting. Particle filters are similar to importance sampling methods [48-50], which are usually used to estimate Bayesian models in which the latent variables are connected in a Markov chain. Particle filters are often an alternative to EKF or UKF with the advantage that, with sufficient samples, they approach the Bayesian optimal estimate, so they can be made more accurate than either the EKF or UKF. However, when the simulated sample is not sufficiently large, they might suffer from sample impoverishment. A few representative types of tasks and methods are selected for easy appreciation of state-of-the-art as shown in Table I.

KF has become a powerful mathematical tool for analyzing and solving localization estimation problems [59;60]. EKF is undoubtedly the most widely used nonlinear state estimation technique in mobile robotics, particularly for localization and mapping problems [61]. About 70% of recent contributions use EKF as the estimation method in robot vision applications.The representative contributions listed in Table I provide a quick understanding of the related works. Further intensive exploration of the literature on our part revealed a review of KF-based SLAM in [62], a comparison of EKF and UKF for data fusion in [58], and an early work on model-based stereo-tracking by KFs in [63]. Of course, the current paper may be the only one that provides an overview of developments on Kalman filters for robot vision.

 

Table I Recent Representatives

Purpose/Task	Method	Representative
Mobile robot localization	EKF for robot localization in an environment	[51]-2009,[52]-2004
Vision-based navigation	EKF for position and orientation estimation	[25]-2010, [4]-2009
Attentional object detection	KF for information integration, parameter adaptation	[53]-2010
Image stabilization	EKF for angle prediction to enhance real-time performance	[34]-2010
Hand-eye calibration	EKF for parameter estimation and optimization	[54]-2008
Real-time tracking	KF combining with echo state network-based self-tuning for face tracking, UKF with a multi-hypotheses tracker for tracking multiple balls	[55]-2010, [56]-2009
Autonomous vehicle	EKF for fast detection and tracking of road curbs	[57]-2004
Visual servoing control	UKF for fusing data from a vision system and an IMU, Iterative Adaptive EKF for noise adaptation and measurement linearization	[23]-2010, [24]-2010
Visual odometry	UKF+RANSAC for structure from motion	[16]-2010, [22]-1998
Pose estimation	EKF for error compensation and information fusion	[7]-2010
Data fusion	EKF/UKF for fusion of inertial and vision data	[58]-2007

 

III.       Typical Formulation for Robot Vision

The basic principle of KF in robot vision is dependent on the minimum mean square error for the optimum estimate and it is adaptive to estimate the state or parameters of stochastic linear discrete systems in vision systems [24;27]. The general procedure of such applications can be described in Fig. 2.

 

Fig. 2. The general procedure of the application of Kalman filters in robot vision.

 

The general problem of KF in robot vision is for estimating the positional state of a controlled action of manipulation or movement, which is governed by the linear stochastic equation (1) with a measurement z_kÎR^m as defined in (2). Denote that the random variables v_k and w_k represent the state and measurement noise, respectively. They are assumed to be independent of each other, white and with normal probability distributions. A is an M´M matrix and H is an N´M matrix. They might change in each step time, but mostly they are assumed to be constant in KF.

 

X_k+1 = AX_k + v_k                                 (1)

z_k = HX_k + w_k                                   (2)

 

Consider the process model for dealing with moving objects in a dynamic robot environment. Generally, from the visual information the motion can be divided into a translation velocity v_x(k) and v_y(k) and a rotation f(k) of the reference frame:

 

X_k = [x(k)  y(k)  v_x(k)  v_x(k)  f(k)]^T        (3)

 

where (x(k), y(k), k) is the current location of a feature point in the image frame, (v_x(k), v_x(k)) is the velocity in x and y directions in the k^th frame, and f(k) is the instantaneous speed of rotation.

Regarding the goal of tracking an object in images, there is another way to represent the initial state of moving objects, i.e.

 

  (4)

 

where S is the tracking window with the size of i´j, (x_k, y_k, k) is the center-of-mass of objects, and  are the translation of x_k and y_k, S_xk and S_yk are the width and length of the tracking window, and  and  are their corresponding translations.

Starting from an initial estimate of the covariance matrix, for each observation z_k, the estimate is updated by

 

                (5)

P_k|k-1 = AP_k-1A^T + Q                  (6)

 

 is the optimal estimate in the last step,  is the prediction at the future step k, A and B are system parameters, U is an optional control input. The error covariance is extrapolated by (6), where P_k|k-1 and P_k-1 are the covariance of X_k|k+1 and X_k-1|k+1, respectively, and Q is the process noise covariance.

During the measurement update, the Kalman gain K_gk is computed by

 

K_gk = P_k|k-1H^T(HP_k|k-1H^T+R)^-1       (7)

    (8)

P_k|k = (I - K_gkH)P_k|k-1                    (9)

 

Using the measured value and the predicted value, an a posteriori state estimate is generated by incorporating the measurement as in (8), i.e. the optimal current state estimate. H is a matrix to relate the state with the measurement z_k. The error covariance estimate is updated by (9).

When the process to be estimated and/or the measurement relationship to the process is non-linear, EKF can be used to linearizes the current mean and covariance. EKF applies the Taylor series approximation to the filtering model so that we can estimate the states even with nonlinear relationship (10). In this case, the measurement equation is represented by (11).

 

X_k = f(X_k-1, u_k-1, v_k-1)            (10)

Z_k = h(X_k, w_k)                      (11)

 

Since the individual values of v_k and w_k cannot be known in each video frame, we can approximate the state and measurement vector by (12)-(15).  is an a posteriori estimate of the state at the k^th frame. X_k and Z_k are the actual state and measurement vectors.  and  are the approximated state and measurement vector.  is an a posteriori estimate of the state at step k. A and V are Jacobian matrices of partial derivatives of function f. H and W are the Jacobian matrices of partial derivatives of function h.

 

 

                       (12)

                                  (13)

     (14)

            (15)

 

In EKF, state estimate and prediction is preformed by (16) and the error covariance is extrapolated by (17). The state estimate update in (18) depends on the measurement Z_k. The Kalman gain is replaced by (19) and the error covariance update is by (20). The matrices A, V, H, and W should be updated with the Jacobians at each time step.

 

 

                               (16)

                   (17)

  (18)

   (19)

                                 (20)

 

Through the algorithms of KF or EKF, the outputs contain the coordinates of object location, the radius or size of the tracking window, and the trajectories of moving objects. The robot uses such information from the visual space to make decision of its operations or actions.

IV.       Tasks and Problems

A.  Robot Localization

Determination of the position and orientation of a vehicle at any time, termed localization, is of paramount importance in achieving reliable and robust autonomous navigation [52;64-67]Achieving high-level tasks such as path planning is possible if the pose is known. Teslic et al. deal with the problem of estimating the output-noise covariance matrix involved in the localization of a mobile robot [68]. A Kalman filter or an EKF is used to localize a mobile robot with a vision sensor within an environment [36;51;69-73]. A maximum incremental probability algorithm for the EKF is formulated in [74] to provide 6D localization and produce a map of planar patches with a convex-hull-based representation.

Correa and Soto present an active perception strategy for a visual sensor mounted on a pan-tilt mechanism [3]. In the standard platform league, substantial sensor limitations exist because of rapid camera motion, limited camera field of view, and limited number of unique landmarks [75]. These limitations place high demands on the performance and robustness of localization algorithms.

SLAM is considered as the key factor in realizing real autonomy for mobile robots [20;21;76-86]. UKF is often applied in SLAM problems because of its direct use of nonlinear models [39]. SLAM is completed by fusing SIFT feature and robot information with EKF [87]. In visual SLAM using an omnidirectional camera, a projection model is needed to unify central catadioptric and conventional cameras. To integrate this model into the EKF-based SLAM, the model is required to linearize the direct and inverse projections [88;89]. An MV-EKF algorithm [38] may also improve the performance.

B.  Pose Estimation

EKF methods can be employed to correct uncertain robot pose [90] or camera pose [48]. Pose is estimated from a set of markers arranged in a known geometry, fused with the measurements of inertial sensors [91]. EKF compensates for the error and fuses the two heterogeneous measurements [7]. The system uses low-cost colored post-it markers, and is capable of handling different frames of reference, as the camera and the inertial unit are mounted on the different mobile subsystems of a sophisticated volant robotic platform. Lippiello et al. deal with the problem of position-based visual servoing in a multi-arm robotic cell (Fig. 3). The approach is based on the real-time estimation of the pose of a target object using the EKF. The data provided by all the cameras are selected according to the prediction of the object self-occlusions, as well as of the mutual occlusions caused by the robot links and tools [19;32;92-94].

 

Fig. 3. Experimental setup for position-based visual servoing in industrial multi-robot cells [92].

For controlling robotic manipulators, the position from a motor encoder is the only sensor measurement for axis control. In this case, accurately estimating the end-effector motion is difficult because of the kinematic errors of links, the joint flexibility of gear mechanisms, and so on. Marayong et al. applied a Kalman filter to integrate the measurements obtained from the camera and encoders to estimate the robot end-effector position [95]. Soo et al. extended the basic idea of the KKF to general rigid body motion, resulting in the formulation of the MD-KKF [43].

C. Visual Measurement

For 3D scene reconstruction from 2D images, localization of 3D points or features in the scene is tracked using KF [96-99]. For modeling unknown environments with a mobile robot, the Mahalanobis-distance is used as the matching criterion, and KF is used to fuse the matching features [22]. Yu et al. propose a high-speed EKF-based approach that recovers camera position and orientation from stereo image sequences without prior knowledge, as well as a procedure for  reconstruction of 3D structures [100-102].

Zhang and Negahdaripour propose an EKF-based recursive dual estimation of stereo data [103;104]. Civera et al. present a combination of EKF and RANSAC, where the available prior probabilistic information from the EKF in the RANSAC model hypothesis stage was used [16].

D. Path Following

A KF or an EKF is commonly used in advanced driver-assistance systems and autonomous navigation systems to track roads over time using image sequences [57;66;105] (Fig. 4). A method is presented in [106] that fuses force and vision in an EKF for following online trajectories. A hybrid force controller is set up to follow a trajectory based on the EKF estimate. Manz et al. describe an approach for tracking autonomous dirt roads [13]. Static road segment estimations are predicted with respect to ego motion, and are fused using Kalman filtering techniques to generate a smooth local clothoid segment for lateral control of the vehicle. To detect the distance and the angle between the robot and the line, a sensor fusion-based line detection is proposed in [107] for unmanned navigations.

 

Fig. 4. Path tracking [105].

 

In a Mars rover studied in [15], the system includes visual odometry, vehicle kinematics, a Kalman filter pose estimator, and a slip-compensated path follower. The Kalman filter processes measurements from an inertial measurement unit and visual odometry. The filter estimate is then compared with the kinematic estimate to determine whether slippage has occurred. The slip vector is calculated from the difference between the current Kalman filter estimate and the kinematic estimate.

For path-tracking controller design in a vision-based wheeled mobile robot, the problem of robot position/orientation tracking control needs to be solved. Two kinematical optimal non-linear predictive control laws are developed in [108] to manipulate the vehicle to follow asymptotically the desired trajectories . A Kalman filter scheme is used to reduce the negative effect of the imaging nose, thereby improving pose estimation accuracy of. To improve vehicle safety during turns and slopes, tracking the ruts formed as a result of vehicle traversal on soft ground are addressed in [109]. The algorithm utilizes an EKF to recursively estimate the parameters of the rut, as well as the relative position and orientation of the vehicle with respect to the rut.

E.  Object Detection and Tracking

Object tracking aims to detect the path of moving objects by obtaining input from a series of images [110;111]. A Kalman filter is used as a prediction module to calculate the motion vectors of moving objects. The filter also tracks the object by assuming the initial state and the noise covariance [46]. Robot vision systems are used for tracking and predicting 3D objects [17;56;112;113], people [114], or planar contours [115] from cameras. For tracking a moving target, a discrete steady-state Kalman filter in [29] calculates the estimated values of the robotic system’s states and the exogenous disturbances. A discrete controller then computes the desired motion of the system.

Face tracking and visual state estimation are often useful in a mobile robot for interaction control, so that it can track a user’s face under several external uncertainties. The robot can also estimate the system state even without the knowledge about a target’s 3D motion-model. This feature is helpful in the development of a real-time visual tracking control system [55]. To develop a robust and friendly human-robot interface system based on natural gestures, an FLC-KF tracking system is presented in [44]. The users are studied and their real-time positions in a dynamic and cluttered working environment are predicted. Similar algorithms can be used for pedestrian localization [2].

A biologically inspired foveated attention system in an object detection scenario is proposed in [53]. An approach to position and orientation estimation for the vision-based navigation of an unmanned aerial vehicle is formulated as a tracking problem and is solved using an EKF [25]. For indoor navigation, the position of a robot is estimated from ceiling landmark images, and is combined with odometric information using an EKF [116].

The EKF is applied in [117] for the nonlinear flight dynamic estimation of a spacecraft, and the effects of the sensor failures are investigated using a bank of Kalman filters. The method detects and decides if and where a sensor fault has occurred, isolates the faulty sensor, and outputs the corresponding healthy sensor measurement.

The state of the leader-follower system is estimated in [26] (Fig. 5), using an EKF as the main estimator [118]. A controller continuously estimates the future position of the leader as it moves, and then directs the follower robot to this position. A Kalman filter is employed for an estimation that uses vision-based measurements of the leader position, a dynamic model of the leader, and a behavioral-cue model of the leader [119]. Once the future position of the leader is estimated, a trajectory planner formulates a path to the future position. On the other hand, a DUKF is implemented in [40] to smoothen measured data and estimate the unknown velocities of the leader.

In medical surgery, robots have significantly helped surgeons to overcome difficulties related to the minimally invasive cardiac surgery procedures. Computer vision techniques can be applied for point-based registration using an EKF. The state estimation is made by the transformation matrix solved by certain decomposition methods. In this case [120], the EKF can quickly converge and avoid being trapped in the local minima of the function. For cardiac surgery, estimating heart motion can be based solely on the natural structures of the heart surface. Occasional surgical instrument occlusions are a challenging problem. An EKF is used for estimating the related series parameters [121]. In surgical robotics, a system needs to compensate for the physiological movements of a target region related to the patient. Tobergte et al. propose a method for accurate robotic motion compensation for a freely moving target object. The target object is equipped with an IMU in addition to tracking markers. Target sensor data is fused by an EKF in a tightly coupled approach. The robot control and the target tracking in the task space aim to combine accuracy, dynamic performance, and robustness with marker occlusions [122].

 

Fig. 5. Vision-based localization for leader-follower control [26]: (a) experimental setup and (b) example result.

 

F.  Multiple Sensors

Multisensor approaches are often adopted in complex robotic tasks [123]. For sensor and information fusion in a robotic soccer team, Silva et al. present a team localization algorithm by integration of visual and compass information [1]. To improve ball position and velocity reliability, the visual sensor noise is studied, and the resulting noise variation is used to define a Kalman filter for ball position. Linear regression is then used for both ball and robot velocity estimation.

A multi-sensor architecture is used to detect moving persons based on the information acquired from a lidar and vision systems [14]. Object detection is performed relative to the estimated robot position. For the lidar and vision systems, classifiers are used and outputs are combined using the Bayesian rule. The estimated person positions are tracked via an EKF. The main aim was to reduce the false positives in the detection process. Georgiev and Allen developed a localization system that uses odometry, a compass and tilt sensor, as well as a global positioning sensor. An EKF integrates the sensor data and keeps track of the uncertainties associated with it [52]. Camera pose estimation plays an important role in the system.

G. Other Purposes

Although image information is one of the most efficient data for robot navigation, it is subject to noise resulting from internal vibration and external factors. Camera vibration decreases image definition by destroying image sharpness, which seriously prevents mobile robots from recognizing their environment for navigation. A robust image stabilization system is proposed for a mobile robot using an EKF [34]. Angle prediction using an EKF enhances the reliability of image analysis for real-time performance. An intelligent gaze control for a vision-guided walking humanoid is presented in [124], where a coupled HEKF is employed for information management.

A Kalman filter is implemented in an autonomous crop treatment robot for localization and crop/weed classification  [65]. Another work [125]  used an EKF for tracking the position and orientation of crop rows. Tuning Kalman filters using self-oscillations are developed in [126] maintaining distances among underwater vehicles. Given the unreliability of measurements, a Kalman filter is designed and unknown dynamic model parameters are determined using simple and time-preserving self-oscillation experiments. A controller is designed based on the Kalman filter estimates. A method is proposed in [127] for real-time detection of bilateral symmetry, which is a salient visual feature of many man-made objects.

In robot vision applications, accurate vision sensor calibration and robust vision-based robot control are essential for developing an intelligent and autonomous system. Motai and Kosaka present an approach to hand-eye robotic calibration for vision-based object modeling and grasping. Intrinsic parameters are optimized by an EKF estimation algorithm to obtain high accuracy [54]. A novel set of image features that yields a rank-efficient image Jacobian for precise 3D positioning of a robotic arm is introduced in [128]. Visual servoing is presented based on an online estimation of the image Jacobian using a Kalman Filter.

V.  Methods and Solutions

A.  Formulation in Robot Vision

Fundamental formulations have been carried out in various studies for pose estimation, tracking, matching, registration, etc. [67;120]. The EKF state and observation models are established by analysis of the imaging geometry of the camera connected with a digital elevation map of the flight area, which helps control estimation error accumulation [25]. For a visual servo using network-synchronized cameras [93], the measurement error variance is directly applied to a Kalman filter. The filter analyzes the feedback from each camera to provide improved position estimates. The filter also models the vision transport delays to provide timely estimates for ensuring the stable and direct visual servoing of a planar robot [94].

To overcome inaccuracies in the direct measurement of joint sensors for robotic manipulation, an MD-KKF is proposed in [43]. An MD-KKF can rapidly and accurately recover the inter-sample values and compensate for the measurement delay of the vision sensor providing the state information of the end-effector. This is done by combining the measurements from the vision sensor, the accelerometers, and the gyroscopes. An MD-KKF is useful in widespread applications such as the high speed visual servo and the high-performance trajectory learning for robot manipulators, as well as in control strategies that require accurate velocity information.

The visual tracking control system in [9] consists of a tracking controller and a visual state estimator. The visual state estimator aimed to estimate the optimal system state and target image velocity, which is used by the visual tracking controller. To achieve this, a self-tuning Kalman filter is proposed to estimate interesting parameters and to overcome the temporary occlusion. A multiple-hypotheses tracker with a UKF is used in each track for handling multiple flying balls, missing and false detections, as well as track initiation and termination [56].

B.  Covariance Estimation

Noise covariances must be optimized for efficient tracking by Kalman filters [92;129]. Ramakoti et al. propose tuning the noise covariances of the Kalman filter for object tracking using particle swarm optimization  [46]. A noise-adaptive variant of the Kalman filter is presented in [17] for the motion estimation and prediction of a free-falling tumbling satellite as seen from a satellite in a neighboring orbit. A discrete-time model of the system that includes the state-transition matrix and the covariance of process noise are effectively derived in a closed form. This derivation is essential for the real-time implementation of the Kalman filter [28].

In [68], the EKF covariances of the observed environment lines, which compose the output-noise covariance matrix in the EKF correction step, are the result of the noise arising from a range-sensor’s distance and angle measurements. The method shows that the use of classic least squares reduces the number of computations in a localization algorithm that is a part of a SLAM algorithm. An MEKF is developed for linearizing the 3D Euclidean motion of lines [35], which does not encounter singularities when computing the Kalman gain and can simultaneously estimate translational and rotational transformations. An MEKF is also used to estimate dynamic motion problems. After a system is calibrated, an MEKF can accurately estimate the relative position.

Regarding square root filters that can ensure covariance matrix non-negative definites, a square-root UKF is introduced into SLAM problem for stability. The algorithm can result in a more accurate estimation compared with a UKF-based SLAM [39;42]. However, the EKF algorithm has its intrinsic disadvantage, such as the divergence in SLAM. An MV-EKF algorithm is proposed in [38] to improve monocular SLAM performance. Indoor image sequence experiments show that the algorithm could improve the convergence of landmarks.

Pornsarayouth and Wongsaisuwan study the sensor fusion of delay and non-delay signals using an KF with a moving covariance [130]. Talu et al. present an approach to detect and isolate sensor failures using a bank of EKFs. These EKFs have an innovative initialization of a covariance matrix using system dynamics [117]. This approach resulted in the development of a fast-convergence Kalman filter algorithm based on the covariance matrix computation for rapid sensor fault detection. The nonlinear filter improved the estimation accuracy by taking advantage of both the fast convergence capability and the robustness of numerical stability.

C. Parameter Optimization

Correa and Soto consider a cost term in an optimization function that favors efficient perceptual actions [3]. Compared with the standard EKF, the results indicate that both robot localization accuracy and efficiency are significantly improved.

For visual servoing, an IA-EKF is proposed in [24] by integrating the mechanisms of noise adaptation with iterative-measurement linearization. An SKF, which introduces three cooperating components, is proposed to overcome the prediction problem [32]. A prediction monitor supervises the prediction quality of an AKF. If a discontinuity is detected, a transition filter attaches to an appropriate steady-state Kalman filter. During this transition, an auxiliary controller ensures continuous overall control.

For attentional object detection with an active vision system [53], top-down information is incrementally estimated and integrated using a Kalman filter, enabling parameter adaptation to changing environments caused by robot locomotion. For modeling and copying human head movements, an iterated EKF is proposed in [131] to linearize within the predicted pose. Proper care was taken to transform the state covariance and incorporated it in a system that can visually recover and track the pose of a human operator’s head.

A method is proposed in SLAM for improving the accuracy of an NN-EKF by compensating for the odometric error of a robot [45]. The NN could adapt to robot systematic errors without any prior knowledge because of its trainability, and SLAM with an NN-aided EKF is more effective than a standard EKF method under colored noise or systematic bias errors.

D. Multiple Models

In some complex tasks, a single Kalman model is inadequate to well solve the problem. For example, a method in [37] utilizes two EKFs to implement SLAM in an underwater environment. The first EKF estimates the local path traveled by the robot and its uncertainty while forming the scan, providing position estimates for correcting distortions in the acoustic images that the vehicle motion produces. The second is an augmented state EKF that estimates and keeps registered scan poses. For SLAM with omnidirectional stereo-vision in [132], using two EKF estimators produces a reliable robot trajectory and a better map of the environment with more landmarks. The first binocular estimator focuses on the robot trajectory. The second monocular estimator is devoted to map building.

From the Robot Soccer World Cup, Quinlan and Middleton [75] found that most of the implemented localization algorithms fall broadly into the class of particle-based filters or Kalman type filters, including the extended and unscented variants. They discuss multiple-model Kalman filters motivated by the RoboCup platform league, and show how they can be used despite the highly multi-modal nature of sensed data. They also give a brief comparison of localizations [123].

An algorithm for estimating 3D localization in an urban environment by fusing measurements from a GPS receiver, an inertial sensor, and vision is presented in [133]. The hybrid sensor is useful for outdoor mobile-augmented reality and 3D robot localization. The approach is developed on the non-linear filtering of these complementary sensors using a multi-rate EKF. A Rao-Blackwellised particle filter for the implementation of monocular SLAM in indoor environments is presented in [49]. The filter is combined with a UKF to sample new poses by integrating current observations. The landmark position estimation is implemented through the unscented transform and EKF.

E.  Information Fusion

The Kalman filter is extremely useful for combining information from multiple heterogeneous sensors [72;134] e.g., vision-lidar fusion [135] or vision and odometric information [116;136]. A real-time face tracking algorithm is proposed based on an adaptive skin color search method to overcome skin color changes caused by light variation [55]. A visual state estimator is also designed by combining a Kalman filter with an echo-state network-based self-tuning algorithm to increase the robustness against colored observation noise. For 3D pose estimation of a volant robot, Kyriakoulis and Gasteratos use low-cost colored post-it markers, apply an EKF to compensate for errors, and fuse the two heterogeneous measurements [7]. The system is computationally inexpensive, operates in real time, and exhibits high accuracy.

Changmook et al. use a vision sensor system and a laser range finder for the unmanned navigation of mobile robots by detecting lines using sensor fusion. Each sensor system runs its own EKF to estimate the distance and orientation of the line [107]. For autonomous stair climbing, an EKF is used for quaternion-based attitude estimation. The rotational velocity measurements from a three-axial gyroscope are fused with the measurements of the stair edges acquired with an onboard camera [137].

The EKF is implemented in [138-141] to fuse information from visual features with odometry, which can extrinsically and automatically calibrate the camera while the robot is moving. The localization algorithm in [36] is based on an HEKF using artificial beacons. The HEKF is proposed to overcome some EKF restraints, such as an absent steady-state solution. Karras et al. present a visual servoing control scheme that is applied to an underwater robotic vehicle [23]. Online estimation of the vehicle states is achieved by fusing data from a laser vision system with an IMU using an asynchronous UKF.

Combining information from force and vision is not straightforward because these sensors are fundamentally different sensory modalities that do not share a common representation. As shown in [106], fusion of tactile and visual measurements enable a highly accurate pose estimation of a moving target. The measurements can be fused together in an EKF by making assumptions on the object shape and sensor uncertainties.

For the fusion of vision and inertial data, the performance of both UKF and EKF are compared in [58]. An EKF can tightly integrate multiple types of visual feature observations with measurements from an IMU [4;15;102;142]. The filter computes accurate estimates of the lander’s terrain-relative position, attitude, and velocity in a resource-adaptive and consequently real-time capable fashion. Other Kalman filters are considered for fusion with IMU data and for a distributed visual landmark matching capability with geometric consistency verification [73;143;144]. A Kalman filter is also used to fuse data from a GPS receiver and a vision system to position a vehicle with respect to objects in its environment [70;145].

VI.       Existing Problems and Future Trends

Although Kalman filters have been developed in many applications as mature approaches for estimation and prediction, some problems still exist in its application in robot vision. Researchers are exerting efforts not only in simple tracking and localization applications, but also in improving the methods mainly in the following aspects.

A.  Real-Time Application and Computational Complexity

Kalman filters have been applied in almost all SLAM systems, which are key research contents in robot autonomous navigation. The visual monocular SLAM based on EKF is an important method of problem handling. However, because of its high computational complexity, it has strict limits on the number and stability of feature points. The traditional method selects a few corners or straight lines as feature points, which limits the application scope of EKF-SLAM. Tamas et al. propose a key-point selection method based on the SIFT feature point, on the assumption of a relatively uniform distribution of feature points. The applied restriction of the visual monocular EKF-SLAM is reduced by effectively controlling the total number of feature points [11]. The computational complexity greatly affects real-time application systems.

B.  Initialization and Reliability

Reliability is a great concern in industrial applications. Vision-based pose estimation in robot control relies on a Kalman filter that requires tuning of filter parameters  [24]. Kalman based techniques rely on existing noise statistics, initial object pose, and sufficiently high sampling rates for a good approximation of measurement-function linearization. Deviations from such assumptions usually lead to degraded pose estimations during visual servoing. Stochastic stability is established in terms of the conditions of the initial estimation error, bound on observation noise covariance, observation nonlinearity, and modeling error. Dynamic features have to be effectively and efficiently treated by their removal from or addition to the filters [103]. New methods should be explored to discard outliers and improve the feature-matching rate. These will help stabilize EKF algorithms and allow more accurate robot localizations or pose estimations.

C. Parametric Constraints

Constraints introduced in Kalman filter parameters may help in some occasions. For example, Kalman filters are commonly used to estimate the states of a mobile vehicle in SLAM in large environments, which incorporate absolute information in a consistent manner. However, the known model or signal information are often either ignored or heuristically dealt with. Another instance is when constraints on state values based on physical considerations are often neglected because they do not easily fit into the structure of the Kalman filter. Cao et al. attempt a rigorous analytical method of incorporating state equality constraints in the Kalman filter [146]. The constraints may vary with time, but they significantly improve the prediction accuracy of the filter. SLAM uses a road-constrained Kalman filter to retain the error in a vehicle’s location and mapping.

D. Efficiency and Accuracy

Efficiency and accuracy are always the most important factors in robot vision. For example, an EKF often requires extensive computations of visual information. Lee et al. attempt an efficient method based on a recursive UKF for a large number of landmarks [41]. The posterior probability distribution of the robot pose is recursively calculated. Each landmark location is updated with the recursively updated robot pose. The method significantly reduces the filtering dimensions and computational complexity. In fact, an EKF for SLAM takes the computational complexity of O(N²) in the map size. A UKF is adopted to improve the handling of non-linearities, but at the expense of O(N³) in the map size, which makes it unattractive for video-rate applications. Van der Merwe and Wan’s general SR-UKF delivers identical results to a general UKF along with computational savings, but overall retained O(N³) [42]. Holmes et al. show how the SR-UKF can be re-posed with O(N²) complexity. Results indicate that the SR-UKF and the UKF produce identical estimates, and that the former is more consistent than the EKF. Huang and Song argue that visual reference scans can be repeatedly used to reduce the computational complexity of an EKF in the SLAM algorithm [147]. Prediction accuracy can, of course, greatly improve system performance.

E.  Integration with Artificial Intelligence

The integration of the Kalman filters with some artificial intelligence methods may yield a better performance. Fuzzy logic, neural network, genetic algorithm, etc. can be combined to wholly resolve a complex task. For example, an NN can be used in estimating the odometric error[45;73;148]. Online learning may be implemented by augmenting the synaptic weights of the NN as the elements of the state vector in the EKF process. A PSO-KF is proven helpful in object tracking [46].

VII.     Conclusion

This paper summarizes recent development in Kalman filter for robotic visual perception. Typical contributions are addressed for localization, surveillance, estimation, search, exploration, navigation, manipulation, tracking, mapping, modeling, etc. Representative works are listed for readers to have a general overview of state-of-the art. A number of methods for solving visual acquisition problems are investigated. More than 20 kinds of methods developed from Kalman filters, extended Kalman filters, and unscented Kalman filters are introduced. In the 50-year history of Kalman filters, they gained entry into the field of robotics in about 30 years. The largest volume of published reports in this literature belongs to the last five years.

 

References

 

[1]     J. Silva, N. Lau, J. Rodrigues, J. Azevedo, and A. Neves, "Sensor and Information Fusion Applied to a Robotic Soccer Team," Robot Soccer World Cup, pp. 366-377, 2010.

[2]     H. S. Ahn and K. H. Ko, "Simple Pedestrian Localization Algorithms Based on Distributed Wireless Sensor Networks," IEEE Trans. Industrial Electronics, vol. 56, no. 10, pp. 4296-4302, 2009.

[3]     J. Correa and A. Soto, "Active Visual Perception for Mobile Robot Localization," Journal of Intelligent & Robotic Systems, vol. 58, no. 3-4, pp. 339-354, 2010.

[4]     A. I. Mourikis, N. Trawny, S. I. Roumeliotis, A. E. Johnson, A. Ansar, and L. Matthies, "Vision-Aided Inertial Navigation for Spacecraft Entry, Descent, and Landing," IEEE Trans. Robotics, vol. 25, no. 2, pp. 264-280, 2009.

[5]     C. Mitsantisuk, S. Katsura, and K. Ohishi, "Kalman-Filter-Based Sensor Integration of Variable Power Assist Control Based on Human Stiffness Estimation," IEEE Trans. Industrial Electronics, vol. 56, no. 10, pp. 3897-3905, Oct.2009.

[6]     K. Szabat, T. Orlowska-Kowalska, and M. Dybkowski, "Indirect Adaptive Control of Induction Motor Drive System With an Elastic Coupling," IEEE Trans. Industrial Electronics, vol. 56, no. 10, pp. 4038-4042, Oct.2009.

[7]     N. Kyriakoulis and A. Gasteratos, "Color-Based Monocular Visuoinertial 3-D Pose Estimation of a Volant Robot," IEEE Trans. Instrumentation and Measurement, vol. 59, no. 10, pp. 2706-2715, 2010.

[8]     B. Larouche, H. Z. Zheng, and S. Meguid, "Development of Autonomous Robot for Space Servicing," 2010 IEEE Int. Conf. on Mechatronics and Automation, pp. 1558-1562, 2010.

[9]     T. Chi-Yi, S. Kai-Tai, X. Dutoit, H. Van Brussel, and M. Nuttin, "Robust visual tracking control system of a mobile robot based on a dual-Jacobian visual interaction model," Robotics and Autonomous Systems, pp. 652-664, 2009.

[10]   C. Chen and C. Yinhang, "MATLAB-based Simulators for Mobile Robot Simultaneous Localization and Mapping," 3rd Int. Conf. on Advanced Computer Theory and Engineering, pp. 576-581, 2010.

[11]   E. Wu, Z. ikun, G. iping, Z. enhui, and W. icong, "Monocular Vision SLAM Based on Key Feature Points Selection," 2010 Int. Conf. on Information and Automation, pp. 1741-1745, 2010.

[12]   E. Muehlenfeld and H. R. Raubenheimer, "Image-Processing with Matched Scanning of Contours," Proceedings of the Society of Photo-Optical Instrumentation Engineers, vol. 397, pp. 125-130, 1983.

[13]   M. Manz, F. von Hundelshausen, and H. Wuensche, "A Hybrid Estimation Approach for Autonomous Dirt Road Following using Multiple Clothoid Segments," 2010 IEEE Int. Conf. on Robotics and Automation, pp. 2410-2415, 2010.

[14]   L. Tamas, M. Popa, G. Lazea, I. Szoke, and A. Majdik, "Lidar and Vision Based People Detection and Tracking," Control Engineering and Applied Informatics, vol. 12, no. 2, pp. 30-35, 2010.

[15]   D. M. Helmick, S. I. Roumeliotis, Y. Cheng, D. S. Clouse, M. Bajracharya, and L. H. Matthies, "Slip-compensated path following for planetary exploration rovers," Advanced Robotics, vol. 20, no. 11, pp. 1257-1280, 2006.

[16]   J. Civera, O. G. Grasa, A. J. Davison, and J. M. M. Montiel, "1-Point RANSAC for Extended Kalman Filtering: Application to Real-Time Structure from Motion and Visual Odometry," Journal of Field Robotics, vol. 27, no. 5, pp. 609-631, 2010.

[17] F. Aghili and K. Parsa, "Adaptive motion estimation of a tumbling satellite using laser-vision data with unknown noise characteristics," 2007 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 839-846, 2007.

[18]   C. Hyeonwoo and W. K. Sang, "Mobile Robot Localization Using Biased Chirp-Spread-Spectrum Ranging," IEEE Trans. Industrial Electronics, vol. 57, no. 8, pp. 2826-2835, Aug.2010.

[19]   J. Pomares and F. Torres, "Movement-flow-based visual servoing and force control fusion for manipulation tasks in unstructured environments," IEEE Trans. Systems Man and Cybernetics Part C-Applications and Reviews, vol. 35, no. 1, pp. 4-15, 2005.

[20]   C. Hyukdoo, Y. K. Dong, P. H. Jae, K. Euntai, and K. Young-Ouk, "CV-SLAM using Ceiling Boundary," 2010 5th IEEE Conf. on Industrial Electronics and Applications, pp. 228-233, 2010.

[21]   I. Mahon, S. B. Williams, O. Pizarro, and M. Johnson-Roberson, "Efficient View-Based SLAM Using Visual Loop Closures," IEEE Trans. Robotics, vol. 24, no. 5, pp. 1002-1014, 2008.

[22]   P. Weckesser and R. Dillmann, "Modeling unknown environments with a mobile robot," Robotics and Autonomous Systems, vol. 23, no. 4, pp. 293-300, 1998.

[23]   G. Karras, S. Loizou, and K. Kyriakopoulos, "A visual-servoing scheme for semi-autonomous operation of an underwater robotic vehicle using an IMU and a Laser Vision System," 2010 IEEE Int. Conf. on Robotics and Automation, pp. 5262-5267, 2010.

[24]   F. Janabi-Sharifi and M. Marey, "A Kalman-Filter-Based Method for Pose Estimation in Visual Servoing," IEEE Trans. Robotics, vol. 26, no. 5, pp. 939-947, 2010.

[25]   J. Zhang, Y. Wu, W. Liu, and X. Chen, "Novel Approach to Position and Orientation Estimation in Vision-Based UAV Navigation," IEEE Trans. Aerospace and Electronic Systems, vol. 46, no. 2, pp. 687-700, 2010.

[26]   G. L. Mariottini, F. Morbidi, D. Prattichizzo, N. V. Valk, N. Michael, G. Pappas, and K. Daniilidis, "Vision-Based Localization for Leader-Follower Formation Control," IEEE Trans. Robotics, vol. 25, no. 6, pp. 1431-1438, 2009.

[27]   G. Welch and G. Bishop, "An Introduction to the Kalman Filter." TR 95-041, University of North Carolina at Chapel Hill, http://portal.acm.org/citation.cfm?id=897831, 2006.

[28]   N. Salvatore, A. Caponio, F. Neri, S. Stasi, and G. L. Cascella, "Optimization of Delayed-State Kalman-Filter-Based Algorithm via Differential Evolution for Sensorless Control of Induction Motors," IEEE Trans. Industrial Electronics, vol. 57, pp. 385-394, 2010.

[29]   N. P. Papanikolopoulos, P. K. Khosla, and T. Kanade, "Visual Tracking of A Moving Target by A Camera Mounted on A Robot - A Combination of Control and Vision," IEEE Trans. Robotics and Automation, vol. 9, no. 1, pp. 14-35, 1993.

[30]   G. Evensen,  Data assimilation : The ensemble Kalman filter. Berlin: Springer, 2007.

[31]   M. D. Butala, R. A. Frazin, Y. G. Chen, and F. Kamalabadi, "Tomographic Imaging of Dynamic Objects With the Ensemble Kalman Filter," IEEE Trans. Image Processing, vol. 18, no. 7, pp. 1573-1587, 2009.

[32]   S. Chroust and M. Vincze, "Improvement of the prediction quality for visual servoing with a switching Kalman filter," Int. J. Robotics Research, vol. 22, no. 10-11, pp. 905-922, 2003.

[33]   C. Perez, N. Garcia, J. M. Sabater, J. M. Azorin, O. Reinoso, and L. Gracia, "Improvement of the visual servoing task with a new trajectory predictor - The Fuzzy Kalman Filter," Fourth Int. Conf. on Informatics in Control, Automation and Robotics, pp. 133-140, 2007.

[34]   W. C. Yun, H. K. Tae, and G. L. Suk, "Development of Image Stabilization System Using Extended Kalman Filter for a Mobile Robot," 2010 Advances in Swarm Intelligence, pp. 675-682, 2010.

[35]   E. Bayro-Corrochano and Y. W. Zhang, "The motor extended Kalman filter: A geometric approach for rigid motion estimation," Journal of Mathematical Imaging and Vision, vol. 13, no. 3, pp. 205-228, 2000.

[36]   H. C. Tran, J. K. Young, and L. Myo-Taeg, "Hybrid extended Kalman filter-based localization with a highly accurate odometry model of a mobile robot," 2008 Int. Conf. on Control, Automation and Systems, pp. 738-743, 2008.

[37]   A. Mallios, P. Ridao, D. Ribas, and E. Herna ndez, "Probabilistic sonar scan matching SLAM for underwater environment," 2010 IEEE Oceans, p. 8, 2010.

[38]   M. Xujiong, H. Feng, and C. Yaowu, "Monocular simultaneous localization and mapping with a modified covariance extended Kalman filter," 2009 IEEE Int. Conf. on Intelligent Computing and Intelligent Systems, pp. 900-903, 2009.

[39]   S. Li and P. Ni, "Square-root unscented Kalman filter based simultaneous localization and mapping," 2010 Int. Conf. on Information and Automation, pp. 2384-2388, 2010.

[40]   Z. F. Li, Y. L. Ma, and T. Ren, "Formation Control of Multiple Mobile Robots Systems," Intelligent Robotics and Applications, vol. 5314, pp. 75-82, 2008.

[41]   S. Lee, S. Lee, and D. Kim, "Recursive unscented Kalman filtering based SLAM using a large number of noisy observations," Int. Journal of Control Automation and Systems, vol. 4, no. 6, pp. 736-747, 2006.

[42]   S. Holmes, G. Klein, and D. Murray, "A square root unscented Kalman filter for visual monoSLAM," 2008 IEEE Int. Conf. on Robotics and Automation, pp. 3710-3716, 2008.

[43]   J. Soo, M. Tomizuka, and T. Katou, "Kinematic Kalman filter (KKF) for robot end-effector sensing," Journal of Dynamic Systems, Measurement and Control, p. 021010, 2009.

[44]   C. Ming-shaung and C. Jung-hua, "A Robust and Friendly Human-robot Interface System Based on Natural Human Gestures," Int. J. Pattern Recognition and Artificial Intelligence, pp. 847-866, 2010.

[45]   K. Jeong-Gwan, A. Su-Yong, and O. Se-Young, "Modified neural network aided EKF based SLAM for improving an accuracy of the feature map," 2010 Int. Joint Conf. on Neural Networks, p. 7, 2010.

[46]   N. Ramakoti, A. Vinay, and R. Jatoth, "Particle swarm optimization aided Kalman filter for object tracking," Int. Conf. on Advances in Computing, Control, & Telecommunication Technologies, pp. 531-533, 2009.

[47]   A. Akrad, M. Hilairet, and D. Diallo, "Design of a Fault-Tolerant Controller Based on Observers for a PMSM Drive," IEEE Trans. Industrial Electronics, vol. 58, no. 4, pp. 1416-1427, Apr.2011.

[48]   F. E. Ababsa and M. Mallem, "Hybrid three-dimensional camera pose estimation using particle filter sensor fusion," Advanced Robotics, vol. 21, no. 1-2, pp. 165-181, 2007.

[49]   M. H. Li, B. R. Hong, and R. H. Luo, "Mobile robot simultaneous localization and mapping using novel Rao-Blackwellised particle filter," Chinese Journal of Electronics, vol. 16, no. 1, pp. 34-39, 2007.

[50]   S. Won, W. W. Melek, and F. Golnaraghi, "A Kalman/Particle Filter-Based Position and Orientation Estimation Method Using a Position Sensor/Inertial Measurement Unit Hybrid System," IEEE Trans. Industrial Electronics, vol. 57, no. 5, pp. 1787-1798, May2010.

[51]   Y. Jingang, W. Hongpeng, Z. Junjie, S. Dezhen, S. Jayasuriya, and L. Jingtai, "Kinematic modeling and analysis of skid-steered mobile robots with applications to low-cost inertial-measurement-unit-based motion estimation," IEEE Trans. Robotics, pp. 1087-1097, 2009.

[52]   A. Georgiev and P. K. Allen, "Localization methods for a mobile robot in urban environments," IEEE Trans. Robotics and Automation, vol. 20, no. 5, pp. 851-864, 2004.

[53]   T. T. Xu, T. G. Zhang, K. Kuhnlenz, and M. Buss, "Attentional Object Detection with An Active Multi-Focal Vision System," Int. Journal of Humanoid Robotics, vol. 7, no. 2, pp. 223-243, 2010.

[54]   Y. Motai and A. Kosaka, "Hand-Eye Calibration Applied to Viewpoint Selection for Robotic Vision," IEEE Trans. Industrial Electronics, vol. 55, no. 10, pp. 3731-3741, 2008.

[55]   C. Y. Tsai, X. Dutoit, K. T. Song, H. Van Brussel, and M. Nuttin, "Robust Face Tracking Control of A Mobile Robot Using Self-Tuning Kalman Filter and Echo State Network," Asian Journal of Control, vol. 12, no. 4, pp. 488-509, 2010.

[56]   O. Birbach and U. Frese, "A Multiple Hypothesis Approach for a Ball Tracking System," 2009 Internationa Conf. on Computer Vision Systems, pp. 435-444, 2009.

[57]   W. S. Wijesoma, K. R. S. Kodagoda, and A. P. Balasuriya, "Road-boundary detection and tracking using ladar sensing," IEEE Trans. Robotics and Automation, vol. 20, no. 3, pp. 456-464, 2004.

[58]   P. Gemeiner, P. Einramhof, and M. Vincze, "Simultaneous motion and structure estimation by fusion of inertial and vision data," Int. Journal of Robotics Research, vol. 26, no. 6, pp. 591-605, 2007.

[59]   E. Manla, A. Nasiri, C. H. Rentel, and M. Hughes, "Modeling of Zinc Bromide Energy Storage for Vehicular Applications," IEEE Trans. Industrial Electronics, vol. 57, pp. 624-632, 2010.

[60]   J. M. Guerrero, J. C. Vasquez, J. Matas, L. G. de Vicuna, and M. Castilla, "Hierarchical Control of Droop-Controlled AC and DC Microgrids - A General Approach Toward Standardization," IEEE Trans. Industrial Electronics, vol. 58, no. 1, pp. 158-172, Jan.2011.

[61]   S. Fazli and L. Kleeman, "Simultaneous landmark classification, localization and map building for an advanced sonar ring," Robotica, vol. 25, pp. 283-296, 2007.

[62]   Z. H. Chen, J. Samarabandu, and R. Rodrigo, "Recent advances in simultaneous localization and map-building using computer vision," Advanced Robotics, vol. 21, no. 3-4, pp. 233-265, 2007.

[63]   M. Tonko and H. H. Nagel, "Model-based stereo-tracking of non-polyhedral objects for automatic disassembly experiments," Int. Journal of Computer Vision, vol. 37, no. 1, pp. 99-118, 2000.

[64]   R. Madhavan and H. F. Durrant-Whyte, "2D map-building and localization in outdoor environments," Journal of Robotic Systems, vol. 22, no. 1, pp. 45-63, 2005.

[65]   B. Southall, T. Hague, J. A. Marchant, and B. F. Buxton, "An autonomous crop treatment robot: Part I. A Kalman filter model for localization and crop/weed classification," Int. Journal of Robotics Research, vol. 21, no. 1, pp. 61-74, 2002.

[66]   Y. Ma, J. Kosecka, and S. S. Sastry, "Vision guided navigation for a nonholonomic mobile robot," IEEE Trans. Robotics and Automation, vol. 15, no. 3, pp. 521-536, 1999.

[67]   D. L. Boley and K. T. Sutherland, "A rapidly converging recursive method for mobile robot localization," Int. Journal of Robotics Research, vol. 17, no. 10, pp. 1027-1039, 1998.

[68]   L. Teslic, I. Skrjanc, and G. Klancar, "Using a LRF sensor in the Kalman-filtering-based localization of a mobile robot," Isa Trans, vol. 49, no. 1, pp. 145-153, 2010.

[69]   A. Weinstein and K. Moore, "Pose Estimation of Ackerman Steering Vehicles for Outdoors Autonomous Navigation," 2010 IEEE Int. Conf. on Industrial Technology, pp. 579-584, 2010.

[70]   A. Rae and O. Basir, "Reducing Multipath Effects in Vehicle Localization by Fusing GPS with Machine Vision," 12Th Int. Conf. on Information Fusion, pp. 2099-2106, 2009.

[71]   L. Se-Jin, L. Jong-Hwan, and C. Dong-Woo, "General Feature Extraction for Mapping and Localization of a Mobile Robot Using Sparsely Sampled Sonar Data," Advanced Robotics, pp. 1601-1616, 2009.

[72]   A. Bais, R. Sablatnig, J. Gu, Y. Khawaja, M. Usman, G. Hasan, and M. Iqbal, "Stereo vision based self-localization of autonomous mobile robots," Proceedings Second Int. Workshop on Robot Vision, pp. 367-380, 2008.

[73]   M. Charkhgard and M. Farrokhi, "State-of-Charge Estimation for Lithium-Ion Batteries Using Neural Networks and EKF," IEEE Trans. Industrial Electronics, vol. 57, pp. 4178-4187, 2010.

[74]   P. de la Puente, D. Rodriguez-Losada, A. Valero, and F. Matia, "3D feature based mapping towards mobile robots' enhanced performance in rescue missions," 2009 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 1138-1143, 2009.

[75]   M. Quinlan and R. Middleton, "Multiple Model Kalman Filters: A Localization Technique for RoboCup Soccer," 2009 Robot Soccer World Cup, pp. 276-287, 2010.

[76]   P. Skrzypczynski, "Simultaneous Localization and Mapping: A Feature-Based Probabilistic Approach," Int. Journal of Applied Mathematics and Computer Science, vol. 19, no. 4, pp. 575-588, 2009.

[77]   L. Armesto, G. Ippoliti, S. Longhi, and J. Tornero, "Probabilistic self-localization and mapping - An asynchronous multirate approach," IEEE Robotics & Automation Magazine, vol. 15, no. 2, pp. 77-88, 2008.

[78]   A. P. Gee, D. Chekhlov, A. Calway, and W. Mayol-Cuevas, "Discovering Higher Level Structure in Visual SLAM," IEEE Trans. Robotics, vol. 24, no. 5, pp. 980-990, 2008.

[79]   J. Sola, A. Monin, M. Devy, and T. Vidal-Calleja, "Fusing Monocular Information in Multicamera SLAM," IEEE Trans. Robotics, vol. 24, no. 5, pp. 958-968, 2008.

[80]   H. Shoudong, W. Zhan, and G. Dissanayake, "Sparse local submap joining filter for building large-scale maps," IEEE Trans. Robotics, pp. 1121-1130, 2008.

[81]   D. Ribas, P. Ridao, J. D. Tardos, and J. Neira, "Underwater SLAM in Man-Made Structured Environments," Journal of Field Robotics, vol. 25, no. 11-12, pp. 898-921, 2008.

[82]   J. Lygouras, V. Kodogiannis, T. Pachidis, and P. Liatsis, "Terrain-Based Navigation for Underwater Vehicles Using an Ultrasonic Scanning System," Advanced Robotics, vol. 22, no. 11, pp. 1181-1205, 2008.

[83]   G. C. Anousaki and K. J. Kyriakopoulos, "Simultaneous localization and map building of skid-steered robots - Ensuring safe movement in structured outdoor environments," IEEE Robotics & Automation Magazine, vol. 14, no. 1, pp. 79-89, 2007.

[84]   M. Bryson and S. Sukkarieh, "Building a robust implementation of bearing-only inertial SLAM for a UAV," Journal of Field Robotics, vol. 24, no. 1-2, pp. 113-143, 2007.

[85]   A. Martinelli, V. Nguyen, N. Tomastis, and R. Siegwart, "A relative map approach to SLAM based on shift and rotation invariants," Robotics and Autonomous Systems, vol. 55, no. 1, pp. 50-61, 2007.

[86]   R. M. Eustice, H. Singh, and J. J. Leonard, "Exactly sparse delayed-state filters for view-based SLAM," IEEE Trans. Robotics, vol. 22, no. 6, pp. 1100-1114, 2006.

[87]   D. Zhu, "Binocular Vision-SLAM Using Improved SIFT Algorithm," 2nd Int. Workshop on Intelligent Systems and Applications, p. 4, 2010.

[88]   A. Rituerto, L. Puig, and J. Guerrero, "Visual SLAM with an omnidirectional camera," 20th Int. Conf. on Pattern Recognition, pp. 348-351, 2010.

[89]   P. Pinies and J. Tardos, "Large-scale SLAM building conditionally independent local maps: application to monocular vision," IEEE Trans. Robotics, pp. 1-13, 2008.

[90]   P. Jaeyong, L. Sukgyu, and J. Park, "Correction robot pose for SLAM based on extended Kalman filter in a rough surface environment," Int. Journal of Advanced Robotic Systems, pp. 67-72, 2009.

[91]   G. Q. Huang, A. B. Rad, Y. K. Wong, and Y. L. Ip, "Heterogeneous multisensor fusion for mapping dynamic environments," Advanced Robotics, vol. 21, no. 5-6, pp. 661-688, 2007.

[92] V. Lippiello, B. Siciliano, and L. Villani, "Position-based visual servoing in industrial multirobot cells using a hybrid camera configuration," IEEE Trans. Robotics, vol. 23, no. 1, pp. 73-86, 2007.

[93]   D. C. Schuurman and D. W. Capson, "Robust direct visual servo using network-synchronized cameras," IEEE Trans. Robotics and Automation, vol. 20, no. 2, pp. 319-334, 2004.

[94]   W. J. Wilson, C. C. W. Hulls, and G. S. Bell, "Relative end-effector control using Cartesian position based visual servoing," IEEE Trans. Robotics and Automation, vol. 12, no. 5, pp. 684-696, 1996.

[95]   P. Marayong, G. D. Hager, and A. M. Okamura, "Control Methods for Guidance Virtual Fixtures in Compliant Human-Machine Interfaces," 2008 IEEE/Rsj Int. Conf. on Robots and Intelligent Systems, pp. 1166-1172, 2008.

[96]   H. Chen-Yu and W. Chieh-Chih, "Scene reconstruction using a pan-tilt-zoom camera with a moving spherical mirror," 2009 ICROS-SICE Int. Joint Conf., pp. 706-711, 2009.

[97]   J. L. Crowley, P. Stelmaszyk, T. Skordas, and P. Puget, "Measurement and Integration of 3-D Structures by Tracking Edge Lines," Int. Journal of Computer Vision, vol. 8, no. 1, pp. 29-52, 1992.

[98]   A. P. Tirumalai, B. G. Schunck, and R. C. Jain, "Dynamic Stereo with Self-Calibration," IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 14, no. 12, pp. 1184-1189, 1992.

[99]   Z. Y. Zhang and O. D. Faugeras, "Estimation of Displacements from 2 3-D Frames Obtained from Stereo," IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 14, no. 12, pp. 1141-1156, 1992.

[100] Y. K. Yu, K. H. Wong, S. H. Or, and M. M. Y. Chang, "Robust 3-D motion tracking from stereo images: A model-less method," IEEE Trans. Instrumentation and Measurement, vol. 57, no. 3, pp. 622-630, 2008.

[101] V. A. Sujan and S. Dubowsky, "Efficient information-based visual robotic mapping in unstructured environments," Int. Journal of Robotics Research, vol. 24, no. 4, pp. 275-293, 2005.

[102] S. G. Chroust and M. Vincze, "Fusion of vision and inertial data for motion and structure estimation," Journal of Robotic Systems, vol. 21, no. 2, pp. 73-83, 2004.

[103] H. S. Zhang and S. Negahdaripour, "EKF-Based Recursive Dual Estimation of Structure and Motion From Stereo Data," IEEE Journal of Oceanic Engineering, vol. 35, no. 2, pp. 424-437, 2010.

[104] L. Matthies, T. Kanade, and R. Szeliski, "Kalman Filter-Based Algorithms for Estimating Depth from Image Sequences," Int. Journal of Computer Vision, vol. 3, no. 3, pp. 209-236, 1989.

[105] M. Asif, M. Arshad, M. Zia, and A. Yahya, "An implementation of active contour and Kalman filter for road tracking," IAENG Int. Journal of Applied Mathematics, pp. 71-77, 2007.

[106] O. Alkkiomaki, V. Kyrki, H. Kalviainen, Y. Liu, and H. Handroos, "Complementing visual tracking of moving targets by fusion of tactile sensing," Robotics and Autonomous Systems, vol. 57, no. 11, pp. 1129-1139, 2009.

[107] C. Changmook, S. SeungBeum, R. Chi-won, K. Yeonsik, K. Sungchul, L. Jung-yup, and H. Chang-soo, "Sensor Fusion-based Line Detection for Unmanned Navigation," 2010 IEEE Intelligent Vehicles Symposium, pp. 191-196, 2010.

[108] J. L. Yang, D. T. Su, Y. S. Shiao, and K. Y. Chang, "Path-tracking controller design and implementation of a vision-based wheeled mobile robot," Proceedings of the Institution of Mechanical Engineers Part I-Journal of Systems and Control Engineering, vol. 223, no. I6, pp. 847-862, 2009.

[109] C. Ordonez, O. Chuy, E. Collins, and L. Xiuwen, "Rut tracking and steering control for autonomous rut following," IEEE Int. Conf. on Systems, Man and Cybernetics, pp. 2775-2781, 2009.

[110] G. S. Gupta, C. H. Messom, and S. Demidenko, "Real-time identification and predictive control of fast mobile robots using global vision sensing," IEEE Trans. Instrumentation and Measurement, vol. 54, no. 1, pp. 200-214, 2005.

[111] S. J. Kim, J. W. Park, and J. M. Lee, "Implementation of tracking and capturing a moving object using a mobile robot," Int. Journal of Control Automation and Systems, vol. 3, no. 3, pp. 444-452, 2005.

[112] J. Zhen, A. Balasuriya, and S. Challa, "Vision based data fusion for autonomous vehicles target tracking using interacting multiple dynamic models," Computer Vision and Image Understanding, pp. 1-21, 2008.

[113] S. C. Sheli and K. Amit, "Vision based target-tracking realized with mobile robots using extended Kalman filter," Engineering Letters, pp. 176-184, 2007.

[114] R. Munoz-Salinas, E. Aguirre, and M. Garcia-Silvente, "People detection and tracking using stereo vision and color," Image and Vision Computing, vol. 25, no. 6, pp. 995-1007, 2007.

[115] M. berich-Carraminana, G. Alenya, J. ndrade-Cetto, E. Martinez, and C. Torras, "Recovering epipolar direction from two affine views of a planar object," Computer Vision and Image Understanding, vol. 112, no. 2, pp. 195-209, 2008.

[116] K. Taeyeon and L. Joon, "Indoor navigation of skid steering mobile robot using ceiling landmarks," 2009 IEEE Int. Symposium on Industrial Electronics, pp. 1743-1748, 2009.

[117] M. F. Talu, S. Soyguder, and O. Aydogmus, "An implementation of a novel vision-based robotic tracking system," Sensor Review, vol. 30, no. 3, pp. 225-232, 2010.

[118] C. N. Teck, M. Adams, and J. Ibanez-Guzman, "Bayesian estimation of follower and leader vehicle poses with a virtual trailer link model," Int. Journal of Robotics Research, pp. 91-106, 2008.

[119] M. Chueh, Y. L. W. A. Yeung, K. P. C. Lei, and S. S. Joshi, "Following controller for autonomous mobile robots using behavioral cues," IEEE Trans. Industrial Electronics, vol. 55, no. 8, pp. 3124-3132, 2008.

[120] S. Zhangjun, X. Jing, Z. Jianwei, and K. Chen, "Point-Based Registration Using Extended Kalman Filter in Medical Robotic System," Proceedings of the 2009 IEEE Int. Conf. on Mechatronics and Automation, pp. 1772-1777, 2009.

[121] R. Richa, A. P. L. Bo , and P. Poignet, "Beating heart motion prediction for robust visual tracking," 2010 IEEE Int. Conf. on Robotics and Automation, pp. 4579-4584, 2010.

[122] A. Tobergte, F. Fro uml hlich, M. Pomarlan, and G. Hirzinger, "Towards Accurate Motion Compensation in Surgical Robotics," 2010 IEEE Int. Conf. on Robotics and Automation, pp. 4566-4572, 2010.

[123] D. Amarasinghe, G. K. I. Mann, and R. G. Gosine, "Landmark detection and localization for mobile robot applications: a multisensor approach," Robotica, vol. 28, pp. 663-673, 2010.

[124] J. F. Seara and G. Schmidt, "Intelligent gaze control for vision-guided humanoid walking: methodological aspects," Robotics and Autonomous Systems, vol. 48, no. 4, pp. 231-248, 2004.

[125] T. Hague and N. D. Tillett, "A bandpass filter-based approach to crop row location and tracking," Mechatronics, vol. 11, no. 1, pp. 1-12, 2001.

[126] N. Miskovic, Z. Vukic, I. Petrovic, and M. Barisic, "Distance keeping for underwater vehicles - tuning Kalman filters using self-oscillations," Oceans 2009, p. 6, 2009.

[127] H. L. Wai, A. Zhang, and L. Kleeman, "Bilateral symmetry detection for real-time robotics applications," Int. Journal of Robotics Research, pp. 785-814, 2008.

[128] C. Kulpate, R. Paranjape, and M. Mehrandezh, "Precise 3D Positioning of A Robotic Arm Using A Single Camera and A Flat Mirror," Int. Journal of Optomechatronics, vol. 2, no. 3, pp. 205-232, 2008.

[129] M. Basin and P. Rodriguez-Ramirez, "Sliding Mode Filter Design for Linear Systems with Unmeasured States," IEEE Trans. Industrial Electronics, vol. 58, no. 8, pp. 3616-3622, 2011.

[130] S. Pornsarayouth and M. Wongsaisuwan, "Sensor fusion of delay and non-delay signal using Kalman Filter with moving covariance," 2008 IEEE Int. Conf. on Robotics and Biomimetics, pp. 2045-2049, 2008.

[131] J. J. Heuring and D. W. Murray, "Modeling and copying human head movements," IEEE Trans. Robotics and Automation, vol. 15, no. 6, pp. 1095-1108, 1999.

[132] T. N. Thanh, Y. Sakaguchi, H. Nagahara, and M. Yachida, "Stereo SLAM using two estimators," 2006 IEEE Int. Conf. on Robotics and Biomimetics, pp. 19-24, 2006.

[133] F. Ababsa, "Advanced 3D localization by fusing measurements from GPS, inertial and vision sensors," IEEE Int. Conf. on Systems, Man and Cybernetics, pp. 871-875, 2009.

[134] J. Forsberg, U. Larsson, and A. Wernersson, "Mobile Robot Navigation Using the Range-Weighted Hough Transform," IEEE Robotics & Automation Magazine, vol. 2, no. 1, pp. 18-26, 1995.

[135] F. Malartre, T. Feraud, C. Debain, and R. Chapuis, "Digital Elevation Map estimation by vision-lidar fusion," 2009 IEEE Int. Conf. on Robotics and Biomimetics, pp. 523-528, 2009.

[136] G. Rui, H. Lei, and C. Xueqi, "Omni-directional vision for robot navigation in substation environments," 2009 IEEE Int. Conf. on Robotics and Biomimetics, pp. 1272-1275, 2009.

[137] A. I. Mourikis, N. Trawny, S. I. Roumeliotis, D. M. Helmick, and L. Matthies, "Autonomous stair climbing for tracked vehicles," Int. Journal of Robotics Research, vol. 26, pp. 737-758, 2007.

[138] D. Scaramuzza, R. Siegwart, and A. Martinelli, "A robust descriptor for tracking vertical lines in omnidirectional images and its use in mobile robotics," Int. Journal of Robotics Research, pp. 149-171, 2009.

[139] J. Goncalves, J. Lima, and P. Costa, "Real-time localization of an omnidirectional mobile robot resorting to odometry and global vision data fusion: an EKF approach," 2008 IEEE Int. Sym. Industrial Electronics, pp. 1275-1280, 2008.

[140] J. S. Yun and J. Miura, "Multi-hypothesis localization with a rough map using multiple visual features for outdoor navigation," Advanced Robotics, vol. 21, no. 11, pp. 1281-1304, 2007.

[141] E. T. Baumgartner and S. B. Skaar, "An Autonomous Vision-Based Mobile Robot," IEEE Trans. Automatic Control, vol. 39, no. 3, pp. 493-502, 1994.

[142] B. Hyun and P. Singla, "Autonomous navigation algorithm for precision landing on unknown planetary surfaces," Advances in the Astronautical Sciences, pp. 1983-2002, 2008.

[143] O. Naroditsky, Z. Zhiwei, A. Das, S. Samarasekera, T. Oskiper, and R. Kumar, "VideoTrek: a vision system for a tag-along robot," 2009 IEEE Computer Society Conf. on Computer Vision and Pattern Recognition Workshops, pp. 1101-1108, 2009.

[144] N. Trawny, A. I. Mourikis, S. I. Roumeliotis, A. E. Johnson, and J. F. Montgomery, "Vision-aided inertial navigation for pin-point landing using observations of mapped landmarks," Journal of Field Robotics, vol. 24, no. 5, pp. 357-378, 2007.

[145] J. Jin-Hwan, H. Dae-Han, K. Yoon-Gu, L. Ho-Geun, L. Ki-Dong, and L. Suk-Gyu, "An enhanced path planning of fast mobile robot based on data fusion of image sensor and GPS," 2009 ICROS-SICE Int. Joint Conf., pp. 5679-5684, 2009.

[146] M. Cao, L. Yu, and P. Cui, "Simultaneous localization and map building using constrained state estimate algorithm," 2008 Chinese Control Conf., pp. 315-319, 2008.

[147] H. Fu-Sheng and S. Kai-Tai, "Vision SLAM using omni-directional visual scan matching," 2008 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, pp. 1588-1593, 2008.

[148] M. Choi, R. Sakthivel, and K. C. Wan, "Neural network-aided extended Kalman filter for SLAM problem," IEEE Int. Conf. on Robotics and Automation, p. 5, 2007.

 

 

 

 

S. Y. Chen (M’01–SM’10) received the Ph.D. degree in computer vision from the Department of Manufacturing Engineering and Engineering Management, City University of Hong Kong, Hong Kong, in 2003.

He joined Zhejiang University of Technology in Feb. 2004 where he is currently a Professor in the College of Computer Science. From Aug. 2006 to Aug. 2007, he received a fellowship from the Alexander von Humboldt Foundation of Germany and worked at University of Hamburg, Germany. From Sep. 2008 to Aug. 2009, he worked as a visiting professor at Imperial College, London, U.K. His research interests include computer vision, 3D modeling, and image processing. Some selected publications and other details can be found at http://www.sychen.com.nu.

Dr. Chen is a senior member of IEEE and a committee member of IET Shanghai Branch. He has published over 100 scientific papers in international journals and conferences. He was awarded as the Champion in 2003 IEEE Region 10 Student Paper Competition, and was nominated as a finalist candidate for 2004 Hong Kong Young Scientist Award.