Sydney, NSW, Australia

nmkwok@unsw.edu.au

Abstract

This paper provides a broad survey on developments of active vision in robotic applications over the last 15 years. With the increasing demand for robotic automation, research in this area has received much attention. Among the many factors that attribute to a high performing robotic system, the planned sensing or acquisition of perceptions on the operating environment is a crucial component. The aim of sensor planning is to determine the pose and settings of vision sensors for undertaking a vision-based task that usually requires obtaining multiple views of the object to be manipulated. Planning for robot vision is a complex problem for an active system due to its sensing uncertainty and environmental uncertainty. This paper describes such problems arising from many applications, e.g. object recognition and modeling, site reconstruction and inspection, surveillance, tracking and search, as well as robotic manipulation and assembly, localization and mapping, navigation and exploration. A bundle of solutions and methods have been proposed to solve these problems in the past. They are summarized in this review while enabling readers to easily refer solution methods for practical applications. Representative contributions, their evaluations, analyses, and future research trends are also addressed in an abstract level.

KEY WORDS— active vision, sensor placement, purposive perception planning, robotics, uncertainty, viewpoint scheduling, computer vision

1. Introduction

About 20 years ago, Bajcsy, Cowan, Kovesi, etc. discussed the important concept of active perception. Together with other researchers' initial contributions at that time, the new concept (compared with the Marr paradigm in 1982) on active perception, and consequently the sensor planning problem, was thus initiated in active vision research. The difference between the concepts of active perception and the Marr paradigm is that the former considers vision perception as the intentional action of the mind, while the latter considers it as the procedural process of the matter.

Therefore, active perception mostly encourages the idea of moving a sensor to constrain interpretation of its environment. Since multiple three-dimensional (3D) images need to be taken and integrated from different vantage points to enable all features of interest to be measured, sensor placement which determines the viewpoints with a viewing strategy thus becomes critically important for achieving full automation and high efficiency. Today, the roles of sensor planning can be widely found in most autonomous robotic systems (Chen, Li & Zhang, 2008a).

Active sensor planning is an important means for fulfilling vision tasks that require intentional actions, e.g. complete reconstruction of an unknown object or dimensional inspection of a workpiece. Constraint analysis, active sensor placement, active sensor configuration, 3D data acquisition, and robot action planning are the essential steps in developing such active vision systems.

Research in active vision is concerned with determining the pose and configuration for the visual sensor, plays an important role in robot vision not only because a 3D sensor has a limited field of view and can only see a portion of a scene from a single viewpoint, but also because a global description of objects often cannot be reconstructed from only one viewpoint due to occlusion. Multiple viewpoints have to be planned for many vision tasks to make the entire object strategically visible.

By taking active actions in robotic perception, the vision sensor is purposefully configured and placed at several positions to observe a target. The intentional actions in purposive perception planning introduce active behaviors or purposeful behaviors. The robots with semantic perception can take intentional actions according to its set goal such as going to a specific location or obtaining the full information of an object. The action to be taken depends on the environment and the robot’s own current state. However, difficulties often arise due to sensor noises and the presence of unanticipated obstacles in the workplace. To this end, a strategic plan is needed to complete a vision task, such as navigating through an office environment or modeling an unknown object.

In this paper, we review the advances in active vision technology broadly. Overall, significant progress has been made in several areas, including new techniques for industrial inspection, object recognition, security and surveillance, site modeling and exploration, multi-sensor coordination, mapping, navigation, tracking, etc. Due to space limitations, this review mainly focuses on the introduction of ideas and high-level strategies.

The scope of this paper is very broad across the field of robotics. The term active vision defined in this paper is equivalent to the situation if and only if the robots have to adopt strategies for decisions of sensor placement (replacement) or sensor configuration (reconfiguration). It can be used for either general purposes, or specific tasks.

Actually, no review of this nature can cite every paper that has been published. We include what we believe to be a representative sampling of important work and broad trends from the recent 15 years. In many cases, we provide references in order to better summarize and draw distinctions among key ideas and approaches. For further information regarding the early contributions in this topic, it is suggested to follow the other intensive review in 1995 (Tarabanis, Allen & Tsai, 1995a).

The remainder of this paper is structured as follows: Section 2 briefly gives an overview of related contributions. Section 3 introduces the tasks, problems, and applications of active vision methods. Section 4 discusses the available methods and solutions to specific tasks. We conclude in Section 5 and offer our impressions of current and future trends on the topic.

2. Overview of Contributions

In the literature, there are about 2000 research papers published during 1986-2010, which are tightly related to the topic of active vision perception in robotics, including sensor modeling and optical constraints, definition of best next view, placement strategy, and illumination planning. The number of 2010 records is not complete since we searched the publications only in the first quarter and most articles have not come into the indexing databases yet. Fig. 1 shows the yearly distribution of the published papers. We can find from the plot that: (1) the subject emerged around 1988 and developed rapidly in the first 10 years, thanks to the new concept of “active vision”; (2) it reaches to the first top in 1998; (3) the subject was cool down a little, probably due to the reasons of many difficulties related to “intelligence”; (4) it became very active again since five years ago because of its wide applications; (5) we are currently on the second peak.

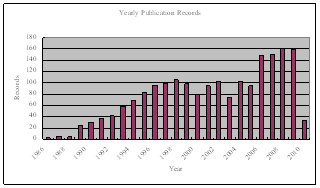
Fig. 1. Yearly published records from 1986 to 2010

With regard to the research themes, there are several directions that researcher had adopted in the past. In Table I, we list several classes that categorize the related work of active vision perception; according to target knowledge, sensor type, task or application, approach, evaluation objective, and planning dimensions.

Table I Categories of active vision applications

Knowledge	model-based	partial	no priori
Sensor	intensity camera	range sensor	both	others
Task	inspection	navigation	modeling	recognition
Approach	generate & test	synthesis	graph	AI
Objective	visibility	accuracy	efficiency	cost
Dimensions	1D	2D	2.5D	3D

2.1. Representative Work

Active vision has very wide applications in robotics. Here we summarize these in the following list where we can find its most significant roles: purposive sensing, object and site modeling, robot localization and mapping, navigation, path planning, exploration, surveillance, tracking, search, recognition, inspection, robotic manipulation, assembly and disassembly, and other purposes.

For the methods used in solving active vision problems, we can also find the tremendous diversity. The mostly used ones are: generate and test, synthesis, sensor simulation, hypothesis and verification, graph theory, cooperative network, space tessellation, geometrical analysis, surface expectation, coverage and occlusion, tagged roadmap, visibility analysis, next best view, volumetric space, probability and entropy, classification and Bayesian reasoning, learning and knowledge-based, sensor structure, dynamic configuration, finite element, gaze and attention, lighting control, fusion, expert system, multi-agent, evolutionary computation, soft computing, fuzzy inference, neural network, basic constraints, and task-driven.

Table II Representative contributions

Purpose/Task	Method	Representative
inspection	constraint analysis	(Trucco, Umasuthan, Wallace & Roberto, 1997; Tarabanis, Tsai & Allen, 1995b; Dunn, Olague & Lutton, 2006)
inspection	genetic algorithm and graph	(Chen & Li, 2004)
surveillance	linear programming, coverage	(Sivaram, Kankanhalli & Ramakrishnan, 2009), (Bottino, Laurentini & Rosano, 2009)
grasping	Kalman filter	(Motai & Kosaka, 2008)
search	probability	(Shubina & Tsotsos, 2010)
tracking	geometrical	(Barreto, Perdigoto, Caseiro & Araujo, 2010)
exploration	uncertainty driven	(Whaite & Ferrie, 1997)
reinforcement learning	reinforcement learning	(Kollar & Roy, 2008, Royer, Lhuillier, Dhome & Lavest, 2007)
site modeling	prediction and verification	(Reed & Allen, 2000; Chang & Park, 2009; Blaer & Allen, 2009; Marchand & Chaumette, 1999b)
object modeling	next best view	(Banta, Wong, Dumont & Abidi, 2000; Chen & Li, 2005; Pito, 1999)
object modeling	information entropy, rule based	(Li & Liu, 2005), (Kutulakos & Dyer, 1995)
recognition	optimal visibility	(de Ruiter, Mackay & Benhabib, 2010)
recognition	probabilistic	(Farshidi, Sirouspour & Kirubarajan, 2009; Roy, Chaudhury & Banerjee, 2005)
path planning	roadmap	(Baumann, Dupuis, Leonard, Croft & Little, 2008; Zhang, Ferrari & Qian, 2009)
general	random occlusion	(Mittal & Davis, 2008)
camera-lighting	geometrical	(Marchand, 2007)
multirobot formation	graph theory	(Kaminka, Schechter-Glick & Sadov, 2008)

Among the huge varieties of tasks and methods, we extract a few representative contributions in Table II for easy appreciation of the state of the art.

2.2. Further Information

For a quick understanding of the related work, it is recommended to read the representative contributions listed in Table II. For further intensive tracking of the literature, the following reviews reflect different aspects of the topic:

(1) Review of active recognition (Arman & Aggarwal, 1993);

(2) Review of industrial inspection (Newman & Jain, 1995);

(3) Review of sensor planning in early stage (Tarabanis et al., 1995a);

(4) Review of 3D shape measurement with active sensing (Chen, Brown & Song, 2000);

(5) Review of surface reconstruction from multiple range images (Zhang, Peng, Shi & Hu, 2000);

(6) Review and comparison of view planning techniques for 3D object reconstruction and inspection (Scott, Roth & Rivest, 2003);

(7) Review of free-form surface inspection techniques (Li & Gu, 2004);

(8) Review of active recognition through next view planning (Roy, Chaudhury & Banerjee, 2004);

(9) Review of 3D measurement quality metrics by environmental factors (MacKinnon, Aitken & Blais, 2008b);

(10) Review of multimodal sensor planning and integration for wide area aurveillance (Abidi, Aragam, Yao & Abidi, 2008);

(11) Review of computer-vision-based fabric defect detection (Kumar, 2008).

Of course, purposive perception planning remains an open problem in the community. The task of finding a suitably small set of sensor poses and configurations for specified reconstruction or inspection goals is extremely important for autonomous robots. The ultimate solution is unlikely existing since the complicated problems always need better solutions along with the development of artificial intelligence.

3. Tasks and Problems

Active vision endows the robot capable of actively placing the sensor at several viewpoints through a planning strategy. It inevitably became a key issue in active systems because the robot had to decide "where to look". In an active vision system, the visual sensor has to be moved frequently for purposeful visual perception. Since the targets may vary in size and distance to the camera and the task requirements may also change in observing different objects or features, a structure-fixed vision sensor is usually insufficient. For a structured light vision sensor, the camera needs to be able to "see" just the scene illuminated by the projector. Therefore the configuration of a vision setup often needs to be changed to reflect the constraints in different views and achieve optimal acquisition performance. On the other hand, a reconfigurable sensor can change its structural parameters to adapt itself to the scene to obtain maximum 3D information from the target. According to task conditions, the problem is roughly classified into two categories, i.e. model-based and non-model-based tasks.

3.1. Model and Non-model based Approaches

For model-based tasks, especially for industrial inspections, the placements of the sensor need to be determined and optimized before carrying out operations. Generally in these tasks, the sensor planning problem is to find a set of admissible viewpoints within the permissible space, which satisfy all of the sensor placement constraints and can complete the required vision task. In most of the related works, the constraints in sensor placement are expressed as a cost function where the planning is aimed at achieving the minimum cost. However, the evaluation of a viewpoint has normally been achieved previously by direct computation. Such an approach is usually formulated for a particular application and is therefore difficult to be applied to general tasks. For a multi-view sensing strategy, global optimization is desired but was rarely considered in the past (Boutarfa, Bouguechal & Emptoz, 2008).

The most typical task of model-based application is for industrial inspection (Yang & Ciarallo, 2001). Along with the CAD model of the target, a sensing plan is generated to completely and accurately acquire the geometry of the target (Olague, 2002; Sheng, Xi, Song & Chen, 2001b). The sensing plan is comprised of the set of viewpoints that defines the exact position and orientation of the camera relative to the target (Prieto, Lepage, Boulanger & Redarce, 2003). Sampling of object surface and viewpoint space is characterized, including measurement and pose errors (Scott, 2009).

For tasks of observing unknown objects or environments, the viewpoints have to be decided in run-time because there is no prior information about the targets. Furthermore, in an inaccessible environment, the vision agent has to be able to take intentional actions automatically. The fundamental objective of sensor placement in such tasks is to increase the knowledge about the unseen portions of the viewing volume while satisfying all placement constraints such as in-focus, field-of-view, occlusion, collision, etc. An optimal viewpoint planning strategy determines each subsequent vantage point and offers the obvious benefit of reducing and eliminating the labor required to acquire an object's surface geometry. A system without planning may need as many as seventy range images for recovering a 3D model with normal complexity, with significant overlap between them. It is possible to reduce the number of sensing operations to less than ten with a proper sensor planning strategy. Furthermore, it also makes it possible to create a more accurate and complete model by utilizing a physics-based model of the vision sensor and its placement strategy.

The most typical task of non-model based application is for target modeling (Banta et al., 2000). Online planning is required to decide where to look (Lang & Jenkin, 2000) for site modeling (Reed & Allen, 2000) or real-time exploration and mapping (Kollar & Roy, 2008). Of the published literature in active vision perception over the years, (Cowan & Kovesi, 1988) is one of the earliest research on this problem in 1988 although some primary works can be found in the period 1985-1987.

To date, there are more than 2000 papers. At the early stage, these works were focused on sensor modeling and constraint analysis. In the first 10 years, most of these research works were model-based and usually for applications in automatic inspection or recognition. The generate-and-test method and the synthesis method are mostly used. In the recent 10 years, while optimization was still in development for model-based problems, the importance is being increasingly realized in planning viewpoints for unknown objects or no a priori environment because this is very useful for many active vision tasks such as site modeling, surveillance, and autonomous navigation. The tasks and problems are summarized in this section separately.

3.2. Purposive Sensing

The purposive sensing in robotic tasks is to obtain better images for robot understanding. Efficiency and accuracy are often primarily concerned in acquisition of 3D images (Chen, Li & Zhang, 2008b; Li & Wee, 2008; Fang, George & Palakal, 2008). Taking the most common example of using stereo image sequences during robot movement, not all input images contribute equally to the quality of the resultant motion. Since several images may often contain similar and hence overly redundant visual information. This leads to unnecessarily increased processing times. On the other hand, a certain degree of redundancy can help to improve the reconstruction in more difficult regions of a model. Hornung et al. proposed an image selection scheme for multi-view stereo which results in improved reconstruction quality compared to uniformly distributed views (Hornung, Zeng & Kobbelt, 2008).

People have also sought methods for determining the probing points for efficient measurement and reconstruction of freeform surfaces (Li & Liu, 2003). For an object that has a large surface or a local steep profile, a variable resolution optical profile measurement system that combined two CCD cameras with zoom lenses, one line laser and a three-axis motion stage was constructed (Tsai & Fan, 2007). The measurement system can flexibly zoom in or out the lens to measure the object profile according to the slope distribution of the object. Model-based simulation system is helpful for planning numerically controlled surface scanning (Wu, Suzuki & Kase, 2005). The scanning-path determination is equivalent to the solution of next best view in this aspect (Sun, Wang, Tao & Chen, 2008).

In order to obtain a minimal error in 3D measurements (MacKinnon, Aitken & Blais, 2008a), an optimization design of the camera network in photogrammetry is useful in 3D reconstruction from several views by triangulation (Olague & Mohr, 2002). The combination of laser scanners and touch probes can potentially lead to more accurate, faster, and denser measurements. To overcome the conflict between efficiency and accuracy, Huang and Qian developed a dynamic sensing-and-modeling approach for integrating a tactile point sensor and an area laser scanner to improve the measurement speed and quality (Huang & Qian, 2007).

Spatial uncertainty and resolution are the primary metrics of image quality; however, spatial uncertainty is affected by a variety of environmental factors. A review of how researchers attempted to quantify these environmental factors can be found in (MacKinnon et al., 2008b), along with spatial uncertainty and resolution, has provided an illustration of a wide range of quality metrics.

For reconstruction in large scenes having large depth ranges with depth discontinuities, an idea is available to integrate coarse-to-fine image acquisition and estimation from multiple cues (Das & Ahuja, 1996).

For construction of realistic models, simultaneous capture of the geometry and texture (Treuillet, Albouy & Lucas, 2007) is inevitable. The quality of the 3D reconstruction depends not only on the complexity of the object but also on its environment. Good viewing and illumination conditions ensure image quality and thus minimize the measurement error. Belhaoua et al. argued the placement problem of lighting sources moving within a virtual geodesic sphere containing the scene, with the aim to find positions leading to minimum errors for the subsequent 3D reconstruction (Belhaoua, Kohler & Hirsch, 2009; Liu, 2009). It is also found that automatic light source placement plays an important role for maximum visual information recovery (Vazquez, 2007).

3.2.1. Object Modeling

In order to reconstruct an object completely and accurately (Shum, Hebert, Ikeuchi & Reddy, 1997; Banta et al., 2000; Lang & Jenkin, 2000; Doi, Sato & Miyake, 2005; Li & Liu, 2005), besides the way is to determine the scanning path (Wang, Zhang & Sun, 2009; Larsson & Kjellander, 2008), multiple images have to be acquired from different views (Pito, 1999). An increasing number of views generally improve the accuracy of the final 3D model but it also increases the time needed to build the model. The number of the possible views can, in principle, be infinite. Therefore, it makes sense to try to reduce the number of needed views to a minimum while preserving a certain accuracy of the model, especially in applications for which the efficiency is an important issue. Approaches to Next View Planning not only can get 3D shapes with minimal views (Sablatnig, Tosovic & Kampel, 2003; Zhou, He & Li, 2008), but also is especially useful for acquisition of large-scale indoor and outdoor scenes (Blaer & Allen, 2007) or interior and exterior model (Null & Sinzinger, 2006), even with partial occlusions (Triebel & Burgard, 2008).

For minimizing the number of images for complete 3D reconstruction where no prior information about the objects is available, in the literature techniques are explored based on characterizing the shapes to be recovered in terms of visibility and number and nature of cavities (He & Li, 2006b; Lin, Liang & Wu, 2007; Loniot, Seulin, Gorria & Meriaudeau, 2007; Chen & Li, 2005; Zetu & Akgunduz, 2005; Pito, 1999).

Typically, Callieri et al. designed a system to reduce the three main bottlenecks in human-assisted 3D scanning: the selection of the range maps to be taken (view planning), the positioning of the scanner in the environment, and the range maps' alignment. The system is designed around a commercial laser-based 3D scanner moved by a robotic arm. The acquisition session is organized in two stages. First, an initial sampling of the surface is performed by automatic selection of a set of views. Then, some added views are automatically selected, acquired and merged to the initial set in order to fill the surface regions left unsampled (Callieri, Fasano, Impoco, Cignoni, Scopigno, Parrini et al. 2004). Similar techniques of free-form surface scanning can be found in (Huang & Qian, 2008b; Huang & Qian, 2008a; Fernandez, Rico, Alvarez, Valino & Mateos, 2008).

The strategy of viewpoint selection for global 3D reconstruction of unknown objects in (Jonnalagadda, Lumia, Starr & Wood, 2003) has four steps: local surface feature extraction, shape classification, viewpoint selection and global reconstruction. An active vision system (Biclops) with two cameras constructed for independent pan/tilt axes, extracts 2D and 3D surface features from the scene. These local features are assembled into simple geometric primitives. The primitives are then classified into shapes, which are used to hypothesize the global shape of the object. The next viewpoint is chosen to verify the hypothesized shape. If the hypothesis is verified, some information about global reconstruction of a model can be stored. If not, the data leading up to this viewpoint is re-examined to create a more consistent hypothesis for the object shape.

Unless using 3D reconstruction from unordered viewpoints (Liang & Wong, 2010), incremental modeling is the common choice for complete automation of scanning an unknown object. An incremental model, representing object surface and workspace occupancy is combined together with an optimization strategy, in selecting the best scanning viewpoints and generates adaptive collision-free scanning trajectories. The optimization strategy attempts to select the viewpoints that maximize the knowledge of the object taking into account the completeness of the current model and the constraints associated with the sensor (Martins, Garcia-Bermejo, Zalama & Peran, 2003).

Most methods for model acquisition require the combination of partial information from different viewpoints in order to obtain a single, coherent model. This, in turn, requires the registration of partial models into a common coordinate frame, a process that is usually done off-line. As a consequence, holes due to undersampling and missing information often cannot be detected until after the registration. Liu and Heidrich introduced a fast, hardware-accelerated method for registering a new view to an existing partial geometric model in a volumetric representation. The method performs roughly one registration every second, and is therefore fast enough for on-the-fly evaluation by the user (Liu & Heidrich, 2003). A procedure is also recently proposed to identify missing areas from the initial scanning data from default positions and to locate additional scanning orientations to fill the missing areas (Chang & Park, 2009). On the contrary, He and Li et al. prefer to a self-determination criterion to inform the robot when the model is complete (He & Li, 2006a; Li, He & Bao, 2005; Li, He, Chen & Bao, 2005).

3.2.2. Site Modeling

It is very time-consuming to construct detailed models of large complex sites by manual process. Therefore, in tasks of modeling unstructured environments (Craciun, Paparoditis & Schmitt, 2008), especially in wide outdoor area, perception planning is required to reduce unobserved portions (Asai, Kanbara & Yokoya, 2007). One of the main drawbacks is determining how to guide the robot and where to place the sensor to obtain complete coverage of a site (Reed & Allen, 2000; Blaer & Allen, 2009). To estimate the computation complexity, if the size of one dimension of the voxel space is n, then there could be O(n²) potential viewing locations. If there are m boundary unseen voxels, the cost of the algorithm could be as high as O(n²´m) (Blaer & Allen, 2009).

For static scenes, the perception-action cycles can be handled at various levels: from the definition of perception strategies for scene exploration down to the automatic generation of camera motions using visual servoing. Marchand and Chaumette use a structure from controlled motion method which allows an optimal estimation of geometrical primitive parameters (Marchand & Chaumette, 1999b). The whole reconstruction/exploration process has three main perception-action cycles (Fig. 2). It contains the internal perception-action cycle which ensures the reconstruction of a single primitive, and a second cycle which ensures the detection, the successive selection, and finally the reconstruction of all the observed primitives. It partially solves the occlusion problem and obtains a high level description of the scene.

In field environments, it is usually not possible to provide robotic systems with valid/complete geometric models of the task and environment. The robot or robot teams will need to create these models by performing appropriate sensor actions. Additionally, the robot(s) will need to position their sensors in a task directed optimum way. The Instant Scene Modeler (iSM) is a vision system for generating calibrated photo-realistic 3D models of unknown environments quickly using stereo image sequences (Se & Jasiobedzki, 2007). Equipped with iSM, unmanned ground vehicles (UGVs) can capture stereo images and create 3D models to be sent back to the base station, while they explore unknown environments. An algorithm based on iterative sensor planning and sensor redundancy is proposed by Sujan et al. to enable robots to efficiently position their cameras with respect to the task/target (Sujan & Dubowsky, 2005a). Intelligent and efficient strategy is developed for unstructured environment (Sujan & Meggiolaro, 2005).

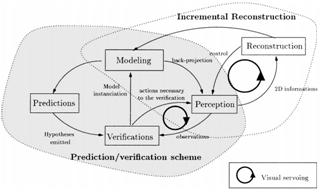
Fig. 2 The Prediction/Verification scheme for scene exploration (Marchand & Chaumette, 1999b)

A field robot for site modeling is usually equipped with ranger sensors, DGPS/Compass, Inertial Measurement Unit (IMU), odometers, etc., e.g. the iSM (Se & Jasiobedzki, 2007). More sensors are set up with the AVENUE, for localizing and navigating itself through various environments (Fig. 3).

3.3. Surveillance

Since vision contains much higher information content than other sensors in describing the scene, cameras are frequently applied for surveillance purposes. In these tasks, cameras can be installed in fixed locations and directed, through pan-tilt manipulations, toward the target in an active manner. On the other hand, cameras can be installed on mobile platforms. Surveillance is also tightly connected with target search and tracking where the active vision principle is regarded as an important attribute.

3.3.1. Surveillance with a set of fixed cameras

This problem was addressed in (Sivaram et al., 2009) concerned with how to select the optimal combination of sensors and how to determine their optimal placement in a surveillance region in order to meet the given performance requirements at a minimal cost for a multimedia surveillance system. Therefore, the sensor configuration for surveillance applications calls for coverage optimization (Janoos, Machiraju, Parent, Davis & Murray, 2007; Yao, Chen, Abidi, Page, Koschan & Abidi, 2010). The goal in such problems is to develop a strategy of network design (Saadatseresht & Varshosaz, 2007).

Locating sensors in 2D can be modeled as an Art Gallery problem (Bottino & Laurentini, 2006b; Howarth, 2005; Bodor, Drenner, Schrater & Papanikolopoulos, 2007). Consider the external visibility coverage for polyhedra under the orthographic viewing model. The problem is to compute whether the whole boundary of a polyhedron is visible from a finite set of view directions, and if so, how to compute a minimal set of such view directions (Liu & Ramani, 2009). Bottino et al. provide detailed formulation and solution in their research (Bottino & Laurentini, 2008; Bottino et al., 2009).

3.3.2. Surveillance with mobile robots

Mobile sensors can be used to provide complete coverage of a surveillance area for a given threat over time, thereby reducing the number of sensors required. The surveillance area may have a given threat profile as determined by the kind of threat, and accompanying meteorological, environmental, and human factors (Ma, Yau, Chin, Rao & Shankar, 2009). UGVs equipped with surveillance cameras present a flexible complement to the numerous stationary sensors being used in security applications today (Hernandez & Wang, 2008; Ulvklo, Nygards, Karlholm & Skoglar, 2004). However, to take full advantage of the flexibility and speed offered by a group of UGV platforms, a fast way to compute desired camera locations to cover an area or a set of buildings, e.g., in response to an alarm, is needed (Nilsson, Ogren & Thunberg, 2009) (Nilsson, Ogren & Thunberg, 2008).

Such surveillance systems aim to design an optimal deployment of vision sensors (Angella, Reithler & Gallesio, 2007; Nayak, Gonzalez-Argueta, Song, Roy-Chowdhury & Tuncel, 2008; Lim, Davis & Mittal, 2006). System reconfiguration is sometimes necessary for the autonomous surveillance of a target as it travels through a multi-object dynamic workspace with an a priori unknown trajectory (Bakhtari, Mackay & Benhabib, 2009; Bakhtari & Benhabib, 2007; Bakhtari, Naish, Eskandari, Croft & Benhabib, 2006).

Autonomous patrolling robots are to have significant contributions in security applications for surveillance purposes (Cassinis & Tampalini, 2007; Briggs & Donald, 2000). In the near future robots will also be used in home environments to provide assistance for the elderly and challenged people (Nikolaidis, Ueda, Hayashi & Arai, 2009; Biegelbauer et al., 2010).

In monitoring applications (Sakane, Kuruma, Omata & Sato, 1995; Mackay & Benhabib, 2008a), Schroeter et al. present a model based system for a mobile robot to find an optimal pose for the observation of a person in indoor living environments. The observation pose is derived from a combination of the camera position and view direction as well as further parameters like the aperture angle. The optimal placement of a camera is required because of the highly dynamic range of the scenes near windows or other bright light sources, which often results in poor image quality due to glare or hard shadows. The method tries to minimize these negative effects by determining an optimal camera pose based on two major models: A spatial free space model and a representation of the lighting (Schroeter, Hoechemer, Mueller & Gross, 2009). A recent review of multimodal sensor planning and integration for wide area surveillance can be found in (Abidi et al., 2008).

3.3.3. Search

Object search is also a model-based vision task which is to find a given object in a known or unknown environment. The object search task not only needs to perform object recognition and localization, but also involves sensing control, environment modeling, and path planning (Wang et al., 2008; Shimizu, Yamamoto, Wang, Satoh, Tanahashi & Niwa, 2005).

The task is often complicated by the fact that portions of the area are hidden from the camera view. Different viewpoints are necessary to observe the target. As a consequence, viewpoint selection for search tasks seems similar to viewpoint selection for data acquisition of an unknown scene. The problem of visual matching was shown to be NP-complete (Ye & Tsotsos, 1999). It has exponential time complexity relative to the size of the image. Suppose one wishes a robot to search for and locate a particular object in a 3D world. A direct search certainly suffices for the solution. Assuming that the target may lie with equal probability at any location, the viewpoint selection problem is resolved by moving a camera to take images of the previously not viewed portions of the full 3D space. This kind of exhaustive, brute-force approach can suffice for a solution; however, it is both computationally and mechanically prohibitive.

In practice, sensor planning is very important for object search since a robot needs to interact intelligently and effectively with the environment. Visual attention may be a mechanism that optimizes the search processes inherent in vision, but attention itself is a complex phenomenon (Shubina & Tsotsos, 2010). The utility of a search operation f is given by

(1)

where t(f) is the time when action f takes. The knowledge about the potential target locations is encoded as a target probability distribution p(c_i,τ). The goal is to select an operation with the highest utility value. Since the cost of each action is approximately the same if the robot is stationary, the next action is selected in such a way that it maximizes the numerator of (1) (Shubina & Tsotsos, 2010).

With the assumption of a realistic, high dimensional and continuous state space for the representation of objects expressing their rotation, translation and class, Eidenberger et al. present an exclusively parametric approach for the state estimation and decision making process to achieve very low computational complexity and short calculation times (Eidenberger, Grundmann, Feiten & Zoellner, 2008).

3.3.4. Tracking

Active tracking is a part of the active vision paradigm (Riggs, Inanc & Weizhong, 2010), where visual systems adapt themselves to the observed environment in order to obtain extra information or perform a task more efficiently. An example of active tracking is fixation, where camera control assures that the gaze direction is maintained on the same object over time. A general approach for the simultaneous tracking of multiple moving targets using a generic active stereo setup is studied in (Barreto et al., 2010). The problem is formulated for objects on a plane, where cameras are modeled as line scan cameras, and targets are described as points with unconstrained motion.

Dynamically reconfigurable vision systems have been suggested in an online mode (Reddi & Loizou, 1995; Wang, Hussein & Erwin, 2008), as effective solutions for achieving this objective, namely, relocating cameras to obtain optimal visibility for a given situation. To obtain optimal visibility of a 3D object of interest, its six DOF position and orientation must be tracked in real time. An autonomous, real-time, six DOF tracking system for a priori unknown objects should be able to (1) select the object, (2) build its approximate 3D model and use this model to (3) track it in real time (de Ruiter et al., 2010).

Zhu and Sakane developed an adaptive panoramic stereovision approach for localizing 3D moving objects (Zhou & Sakane, 2003). The research focuses on cooperative robots involving cameras that can be dynamically composed into a virtual stereovision system with a flexible baseline in order to detect, track, and localize moving human subjects in an unknown indoor environment. It promises an effective way to solve the problems of limited resources, view planning, occlusion, and motion detection of movable robotic platforms. Theoretically, two interesting conclusions are given. (1) If the distance from the main camera to the target, D₁, is significantly greater (e.g., ten times greater) than the size of the robot (R), the best geometric configuration is

(2)

where B is the best baseline distance for minimum distance error and f₁ is the main camera’s inner angle of the triangle formed by the two robots and the target. (2) The depth error of the adaptive stereovision is proportional to D^1.5 where D is the camera-target distance, which is better than the case of the best possible fixed baseline stereo in which depth error is proportional to the square of the distance (D²).

Some problems like camera fixation, object capturing and detecting, and road following involve tracking or fixating on 3D points and features (Biegelbauer, Vincze & Wohlkinger, 2010). The solutions to these problems also require an analysis of depth and motion. Theoretical approaches based on optical flow are the most common solution to these problems (Han, Choi & Lee, 2008; Raviv & Herman, 1994).

Vision tracking systems for surveillance and motion capture rely on a set of cameras to sense the environment (Chen & Davis, 2008). There is a decision problem which corresponds to answering the question: can the target escape the observer’s view? Murrieta-Cid et al. defined this problem and considered to maintain surveillance of a moving target by a nonholonomic mobile observer (Murrieta-Cid, Muoz & Alencastre, 2005). The observer's goal is to maintain visibility of the target from a predefined, fixed distance. An expression derived for the target velocities is:

(3)

where q and f are the observer’s orientation, u₁ and u₃ are moving speeds, and l is the predefined surveillance distance.

To maintain the fixed required distance between the target and the observer, the relationship between the velocity of the target and the linear velocity of the observer is

(4)

The above equation defines an ellipse in the u₁-u₃ plane and the constraint on u₁ and u₃ is that they should be inside the ellipse while supposing. They deal specifically with the situation in which the only constraint on the target's velocity is a bound on the speed, and the observer is a nonholonomic, differential drive system having bounded speed. The system model is developed to derive a lower bound for the required observer speed.

To dynamically manage the viewpoint of a vision system for optimal 3D tracking, Chen and Li adopt the effective sample size in the proposed particle filter as a criterion for evaluating tracking performance and employ it to guide the view-planning process for finding the best viewpoint configuration. The vision system is designed and configured to maintain a largest number of effective particles, which minimizes tracking error by revealing the system to a better swarm of importance samples and interpreting posterior states in a better way (Chen & Li, 2009; Chen & Li, 2008).

3.4. Mobile Robotics

In applications involving the deployment of mobile robots, it is a fundamental requirement that the robot is able to take perception of its navigation environment. When cameras are equipped on mobile robots, it enables the robot to observe its workspace and active vision naturally becomes a very desirable ability to improve the autonomy of these machines.

3.4.1. Localization and Mapping

As a problem of determining the position of a robot or its vision sensor, localization has been recognized as one of the most fundamental problems in mobile robotics (Caglioti, 2001; Flandin & Chaumette, 2002). Mobile robots often determine their actions according to their positions. Thus, their observation strategies are mainly for self-localization (Mitsunaga & Asada, 2006). The aim of localization is to estimate the position of a robot in its environment, given local sensorial data. Stereo vision-based 3D localization is used in a semi-automated excavation system for partially buried objects in unstructured environments by (Maruyama, Takase, Kawai, Yoshimi, Takahashi & Tomita, 2010). Autonomous navigation is also possible in outdoor situations with the use of a single camera and natural landmarks (Royer et al., 2007; Chang, Chou & Wu, 2010).

Fig. 3 The ATRV-2 AVENUE-based mobile robot for site modeling (Blaer & Allen, 2009)

Zingaretti and Frontoni present an efficient metric for appearance-based robot localization (Zingaretti & Frontoni, 2006). This metric is integrated in a framework that uses a partially observable Markov decision process as position evaluator, thus allowing good results even in partially explored environments and in highly perceptually aliased indoor scenarios. More details of this topic are related to the research on simultaneous localization and mapping (SLAM) which is also a challenging problem and has been widely investigated (Borrmann, Elseberg, Lingemann, Nüchter & Hertzberg, 2008; Borrmann et al., 2008; Frintrop & Jensfelt, 2008a; Nüchter & Hertzberg, 2008; Gonzalez-Banos & Latombe, 2002).

In intelligent transportation systems, vehicle localization usually relies on Global Positioning System (GPS) technology; however the accuracy and reliability of GPS are degraded in urban environments due to satellite visibility and multipath effects. Fusion of data from a GPS receiver and a machine vision system can help to position the vehicle with respect to objects in its environment (Rae & Basir, 2009).

In robotics, maps are metrical and sometimes topological. A map contains space-related information about the environment, i.e., not all that a robot may know or learn about its world need go into the map. Metric maps are supposed to represent the environment geometry quantitatively correctly, up to discretization errors (Nüchter & Hertzberg, 2008).

Again for the SLAM problem (Kaess & Dellaert, 2010; Ballesta, Gil, Reinoso, Julia & Jimenez, 2010), the goal is to integrate the information collected during navigation into the most accurate map possible. However, SLAM does not address the sensor-placement portion of the map-building task. That is, given the map built so far where should the robot go next? In (Gonzalez-Banos & Latombe, 2002), an algorithm is proposed to guide the robot through a series of "good" positions, where "good" refers to the expected amount and quality of the information that will be revealed at each new location. This is similar to the next-best-view, (NBV) problem. However, in mobile robotics the problem is complicated by several issues, two of which are particularly crucial. One is to achieve safe navigation despite an incomplete knowledge of the environment and sensor limitations. The other is the need to ensure sufficient overlap between each new local model and the current map, in order to allow registration of successive views under positioning uncertainties inherent to mobile robots. They described an NBV algorithm that uses the safe-region concept to select the next robot position at each step. The new position is chosen within the safe region in order to maximize the expected gain of information under the constraint that the local model at this new position must maintain a minimal overlap with the current global map (Gonzalez-Banos & Latombe, 2002).

Besides individual scans are registered into a coherent 3D geometry map by SLAM, semantic knowledge can help an autonomous robot act goal-directedly, then, consequently, part of this knowledge has to be related to objects, functionalities, events, or relations in the robot's environment. A semantic map for a mobile robot is a map that contains, in addition to spatial information about the environment, assignments of mapped features to entities of known classes (Nüchter & Hertzberg, 2008).

While considerable progress has been made in the area of mobile networks by SLAM or NBV, a framework that allows the vehicles to reconstruct target based on a severely underdetermined data set is rarely addressed. Recently, Mostofi and Sen present a compressive cooperative mapping framework for mobile exploratory networks. The cooperative mapping of a spatial function is based on a considerably small observation set where a large percentage of the area of interest is not sensed directly (Mostofi & Sen, 2009).

3.4.2. Navigation, Path Planning and Exploration

For exploring unknown environments, many robotic systems use topological structures as a spatial representation. If localization is done by estimate of the global pose from landmark information, robotic navigation is tightly coupled to metric knowledge. On the other hand, if localization is based on weaker constraints, e.g. the similarity between images capturing the appearance of places or landmarks, the navigation can be controlled by a homing algorithm. Similarity based localization can be scaled to continuous metric localization by adding additional constraints (Hubner & Mallot, 2007; Baker & Kamgar-Parsi, 2010; Hovland & McCarragher, 1999; Whaite & Ferrie, 1997; Sheng, Xi, Song & Chen, 2001a; Kim & Cho, 2003).

If the environment is partially unknown, the robot needs to explore its work-space autonomously. Its task is to incrementally build up a representation of its surroundings (Suppa & Hirzinger, 2007; Wang & Gupta, 2007). Local navigation strategy has to be implemented for unknown environment exploration (Amin, Tanoto, Witkowski, Ruckert & bdel-Wahab, 2008; Thielemann, Breivik & Berge, 2010; Radovnikovich, Vempaty & Cheok, 2010).

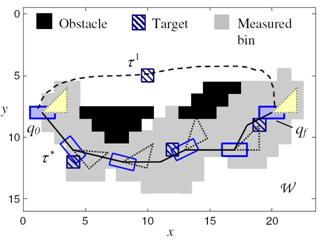
Fig. 4 An example of sensor path planning (Zhang et al., 2009), where both the location and geometry of targets and obstacles must be accounted for in planning the sensor path.

For navigation in an active way, an UGV is usually equipped with a “controllable” vision head, e.g. a stereo camera on pan/tilt mount (Borenstein, Borrell, Miller & Thomas, 2010; Banish, Rodgers, Hyatt, Edmondson, Chenault, Heym et al. 2010). Kristensen presented the problem of autonomous navigation in partly known environments (Kristensen, 1997). Bayesian decision theory was adopted in the sensor planning approach. The sensor modalities, tasks, and modules were described separately and Bayes decision rule was used to guide the behavior. The decision problem for one sensor was constructed with a standard tree for myopic decision. In other aspects, indoor navigation using adaptive neuro-fuzzy controller is addressed in (Budiharto, Jazidie & Purwanto, 2010) and path recognition for outdoor navigation is addressed in (Shinzato, Fernandes, Osorio & Wolf, 2010).

The problem of path planning for a robotic sensor in (Zhang et al., 2009) is assumed with a platform geometry AÌR², and a field-of-view geometry SÌR², that navigates a workspace WÌR² for the purpose of classifying multiple fixed targets based on posterior and prior sensor measurements, and environmental information (Fig. 4). The robotic sensor path τ must simultaneously achieve multiple objectives including: (1) avoid all obstacles in W; (2) minimize the traveled distance; and (3) maximize the information value of path (τ), i.e. the measurement set along a path τ. The robotic sensor performance is defined by an additive reward function:

R(τ) = w_V V(τ) − w_D D(τ) (5)

where, V(τ) is the information value of path (τ), and D(τ) is the distance traveled along τ. The constants w_V and w_D weigh the trade-off between the values of the measurements and the traveled distance. Then, the Geometric Sensor Path Planning Problem is defined as:

Problem: Given a layout W and a joint probability mass function P, find a path τ* for a robotic sensor with platform A and field-of-view S that connects the two ends, and maximizes the profit of information defined in (1) (Zhang et al., 2009).

In active perception for exploration, navigation, or path planning, there is a situation that the robot has to work in a dynamic environment and the sensing process may associate with many noises or uncertainties. Research in this issue has become the most active in recent years. A reinforcement learning scheme is proposed for exploration in (Kollar & Roy, 2008). Occlusion-free path planning are studied in (Baumann et al., 2008; Nabbe & Hebert, 2007; Baumann, Leonard, Croft & Little, 2010; Oniga & Nedevschi, 2010).

3.5. Robotic Manipulations

The use of robotic manipulators had shown a boost in manufacturing productivity. This increase depends critically on the simplicity that the robot manipulator can be re-configured or re-programmed to perform various tasks. To this end, actively placing the camera to guide the manipulator motion has become a key component of automatic robotic manipulator systems.

3.5.1. Robotic Manipulation

Vision guided approaches are designed to robustly achieve high precision in manipulation (Nickels, DiCicco, Bajracharya & Backes, 2010; Miura & Ikeuchi, 1998) or to improve the productivity (Park et al., 2006). For the assembly/disassembly tasks, a long-term aim in robot programming is the automation of the complete process chain, i.e. from planning to execution. One challenge is to provide solutions which are able to deal with position uncertainties (Fig. 5) (Thomas, Molkenstruck, Iser & Wahl, 2007). Nelson et al. introduced a dynamic sensor planning method (Nelson & Papanikolopoulos, 1996). They used an eye-in-hand system and considered the resolution, field-of-view, depth-of-view, occlusions, and kinematic singularities. A controller was proposed to combine all the constraints into a system and resulted in a control law. Kececi et al. employed an independently mobile camera with a 6-DOF robot to monitor a disassembly process so that it can be planned (Kececi et al., 1998). A number of candidate view-poses are being generated and subsequently evaluated to determine an optimal view pose. A good view-pose is defined with the criterion which prevents possible collisions, minimizes mutual occlusions, keeps all pursued objects within the field-of-view, and reduces uncertainties.

Stemmer et al. used a vision sensor, with color segmentation and affine invariant feature classification, to provide the position estimation within the region of attraction (ROA) of a compliance-based assembly strategy (Stemmer, Schreiber, Arbter & Albu-Schaffer, 2006). An assembly planning toolbox is based on a theoretical analysis and the maximization of the ROA. This guarantees the local convergence of the assembly process under consideration of the geometry in part. The convergence analysis invokes the passivity properties of the robot and the environment.

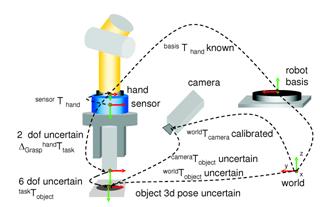
Fig. 5 Vision sensor for solving object poses and uncertainties in the assembly work cell (Thomas et al., 2007)

Object verification (Sun, Sun & Surgenor, 2007), feature detectability (Zussman, Schuler & Seliger, 1994), and real-time accessibility analysis for robotic (Jang, Moradi, Lee, Jang, Kim & Han, 2007) are also major concerns in robotic manipulation. The access direction of the object to grasp can be determined through visibility query (Jang, Moradi, Le Minh, Lee & Han, 2008; Motai & Kosaka, 2008).

3.5.2. Recognition

In many cases, a single view may not contain sufficient features to recognize an object unambiguously (Byun & Nagata, 1996). Therefore, another important application of sensor planning is active object recognition (AOR) which recently attracts much attention within the computer vision community.

In fact, two objects may have all views in common with respect to a given feature set, and may be distinguished only through a sequence of views (Roy, Chaudhury & Banerjee, 2000). Further, in recognizing 3D objects from a single view, recognition systems often use complex feature sets. Sometimes, it may be possible to achieve the same result, incurring less error and smaller processing cost by using a simpler feature set and suitably planning multiple observations. A simple feature set is applicable for a larger class of objects than a model base with a specific complex feature set. Model base-specific complex features such as 3D invariants have been proposed only for special cases. The purpose of AOR is to investigate the use of suitably planned multiple views for 3D object recognition. Hence the AOR system should also take a decision on "where to look". The system developed by Roy et al. is an iterative active perception system that executes the acquisition of several views of the object, builds a stochastic 3D model of the object and decides the best next view to be acquired (Roy et al., 2005).

In computer vision, object recognition problems are often based on single image data processing (SyedaMahmood, 1997; Eggert, Stark & Bowyer, 1995). In various applications this processing can be extended to a complete sequence of images, usually received passively. In (Deinzer, Derichs, Niemann & Denzler, 2009), a camera is selectively moved around a target object. Reliable classification results are desirable with a clearly reduced amount of necessary views by optimizing the camera movement for the access of new viewpoints. The optimization criterion is the gain of class discriminative information when observing the appropriate next image (Roy et al., 2000; Gremban & Ikeuchi, 1994).

While relevant research in active object recognition/pose estimation has mostly focused on single-camera systems, Farshidi et al. propose two multi-camera solutions that can enhance object recognition rate, particularly in the presence of occlusion. Multiple cameras simultaneously acquire images from different view angles of an unknown, randomly occluded object belonging to a set of a priori known objects (Farshidi et al., 2009). Eight objects, as illustrated in Fig. 6, are considered in the experiments with four different pose angles, each 90^O apart. Also, five different levels of occlusion have been designated for each camera’s image.

Fig. 6 The objects for active recognition experiments (Farshidi et al., 2009)

In the early stage, Ikeuchi et al. developed a sensor modeler, called VANTAGE, to place the light sources and cameras for object recognition (Ikeuchi & Robert, 1991; Wheeler & Ikeuchi, 1995). It mostly solves the detectability (visibility) of both light sources and cameras. Borotschnig summarized a framework for appearance-based AOR as in Fig. 7 (Borotschnig & Paletta, 2000).

Among the literature of recognition, many solutions are available (Dickinson, Christensen, Tsotsos & Olofsson, 1997; Arman & Aggarwal, 1993; Kuno, Okamoto & Okada, 1991; Callari & Ferrie, 2001). Typically, we may refer to the fast recognition by learning (Grewe & Kak, 1995) and function-based reasoning (Sutton & Stark, 2008), as well as multi-view recognition of time-varying geometry objects (Mackay & Benhabib, 2008b). A review of sensor planning for active recognition can be found in (Roy et al., 2004).

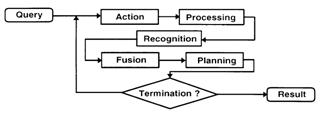
Fig. 7 The framework of appearance-based active object recognition (Borotschnig & Paletta, 2000)

3.5.3. Inspection

Dimensional inspection using a contact-based coordinate measurement machine is time consuming because the part can only be measured on a point-by-point basis (Prieto, Redarce, Lepage & Boulanger, 2002). The automotive industry has been seeking a practical solution for rapid surface inspection using a 3D sensor. The challenge is the capability to meet all the requirements including sensor accuracy, resolution, system efficiency, and system cost. A robot-aided sensing system can automatically allocate sensor viewing points, measure the freeform part surface, and generate an error map for quality control (Shi, Xi & Zhang, 2010; Shih & Gerhardt, 2006; Bardon, Hodge & Kamel, 2004). Geometric dimension and tolerance inspection process is also needed in industries to examine the conformity of manufactured parts with the part specification defined at the design stage (Gao, Gindy & Chen, 2006; Sebastian, Garcia, Traslosheros, Sanchez & Dominguez, 2007).

In fact, in the literature, sensor planning for the model-based tasks is mostly related to industrial inspection, where a nearly perfect estimate of the object's geometry and possibly its pose are known and the task is to determine how accurately the object has been manufactured (Mason, 1997; Trucco et al., 1997; Sheng et al., 2001b; Yang & Ciarallo, 2001; Wong & Kamel, 2004; Sheng, Xi, Song & Chen, 2003). It was said that this problem in fact was a nonlinear multi-constraint optimization problem (Chen & Li, 2004; Taylor & Spletzer, 2007; Rivera-Rios, Shih & Marefat, 2005; Dunn & Olague, 2004). The problem comprises camera, robot and environmental constraints. A viewpoint is optimized and evaluated by a cost function which uses a probability-based global search technique. It is difficult to compute robust viewpoints which satisfy all feature detectability constraints. Optimization methods such as tree annealing and genetic algorithms are commonly used to compute the viewpoints subjected to multi-constraints (Chen & Li, 2004; Olague & Mohr, 2002; Olague & Dunn, 2007).

Tarabanis et al. developed a model-based sensor planning system, the machine vision planner (MVP), which works with 2D images obtained from a CCD camera (Tarabanis, Tsai & Kaul, 1996; Tarabanis et al., 1995b). The MVP system takes a synthesis rather than a generate-and-test approach, thus giving rise to a powerful characterization of the problem. In addition, the MVP system provides an optimization framework in which constraints can easily be incorporated and combined. The MVP system attempts to detect several features of interest in the environment that are simultaneously visible, inside the field of view, in focus, and magnified, by determining the domain of admissible camera locations, orientations, and optical settings. A viewpoint is sought that is both globally admissible and central to the admissibility domain (Fig. 8).

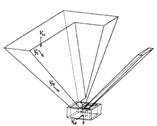
Fig. 8 The admissible domain of viewpoints (Tarabanis et al., 1995b)

Based on the work on the MVP system, Abrams et. al. made a further development for planning viewpoints for vision inspection tasks within a robot work-cell (Abrams, Allen & Tarabanis, 1999). The computed viewpoints met several constraints such as detectability, in-focus, field-of-view, visibility, and resolution. The proposed viewpoint computation algorithm also fell into the "volume intersection method" (VIM). This is generally a straightforward but very useful idea. Many of the latest implemented planning systems can be traced back to this contribution. For example, Rivera-Rios et al. present a probabilistic analysis of the effect of the localization errors on the dimensional measurements of the line entities for a parallel stereo setup (Fig. 9). The probability that the measurement error is within an acceptable tolerance was formulated as the selection criterion for camera poses. The camera poses were obtained via a nonlinear program that minimizes the total mean square error of the length measurements while satisfying the sensor constraints (Rivera-Rios et al., 2005).

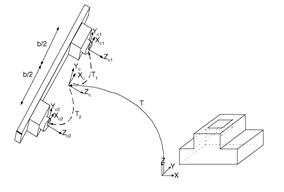
Fig. 9 Stereo pose determination for dimensional measurement (Rivera-Rios et al., 2005)

In order to obtain a more complete and accurate 3D image of an object, Prieto et al. presented an automated acquisition planning strategy utilizing its CAD model. The work was focused on improving the accuracy of the 3D measured points which is a function of the distance to the object surface and of the laser beam incident angle (Prieto, Redarce, Boulanger & Lepage, 2001; Prieto et al., 2003).

Besides the minimum number of viewpoints is desired in sensor planning, to further improve the efficiency of robot manipulation, we need to reduce the traveling cost of the robot placements (Wang, Krishnamurti & Gupta, 2007; Martins, Garcia-Bermejo, Casanova & Gonzalez, 2005; Chen & Li, 2004). The whole procedure for generating a perception plan is described as: (1) generate a number of viewpoints; (2) reduce redundant viewpoints; (3) if the placement constraints are not satisfied, increase the number of viewpoints; (4) construct a graph corresponding to the space distribution of the viewpoints; and (5) find a shortest path to optimize robot operations.

Automated visual inspection systems are also developed for defect inspection, such as specular surface quality control (Garcia-Chamizo, Fuster-Guillo & zorin-Lopez, 2007), car headlight lens inspection (Martinez, Ortega, Garcia & Garcia, 2008), and others (Perng, Chen & Chang, 2010; Martinez, Ortega, Garcia & Garcia, 2009; Chen & Liao, 2009; Sun, Tseng & Chen, 2010). Related techniques are useful to improve the productivity of assembly lines (Park, Kim & Kim, 2006). Self-reconfiguration (Garcia & Villalobos, 2007a; Garcia & Villalobos, 2007b) and self-calibration (Carrasco & Mery, 2007; Treuillet, Albouy & Lucas, 2009) are also mentioned in some applications. Further information regarding early literatures can be found in the review by (Newman & Jain, 1995).

3.6. General Purpose Tasks

The automatic selection of good viewing parameters is a very complex problem. In most cases the notion of good viewing strongly depends on the concrete application, but some general solutions still exist in a limited extent (Chu & Chung, 2002; Zavidovique & Reynaud, 2007). Commonly, two kinds of viewing parameters must be set for active vision perception: camera parameters and lighting parameters (number of light sources, its position and eventually the orientation of the spot). The former determine how much of the geometry can be captured and the latter influence on how much of it is revealed (Vazquez, 2007).

Some multiview strategies are proposed for different application prospects (Al-Hmouz & Challa, 2005; Fiore, Somasundaram, Drenner & Papanikolopoulos, 2008). Mittal specifically addressed the state-of-the-art in the analysis of scenarios where there are dynamically occurring objects capable of occluding each other. The visibility constraints for such scenarios are analyzed in a multi-camera setting. Also analyzed are other static constraints such as image resolution and field-of-view, and algorithmic requirements such as stereo reconstruction, face detection and background appearance. Theoretical analysis with the proper integration of such visibility and static constraints leads to a generic framework for sensor planning, which can then be customized for a particular task. The analysis may be applied to a variety of applications, especially those involving randomly occurring objects, and include surveillance and industrial automation (Mittal, 2006).

In some robotic vision tasks, such as surveillance, inspection, image based rendering, environment modeling, require multiple sensor locations, or the displacement of a sensor in multiple positions for fully exploring an environment or an object. Edge covering is sufficient for tasks such as inspection or image based rendering. However, the problem is NP-hard, and no finite algorithm is known for its exact solution. A number of heuristics have been proposed, but their performances with respect to optimality are not guaranteed (Bottino et al., 2009). In 2D surveillance, the problem is modeled as an Art Gallery problem. A subclass of this general problem can be formulated in terms of planar regions that are typical of building floor plans. Given a floor plan to be observed, the problem is then to reliably compute a camera layout such that certain task-specific constraints are met. A solution to this problem is obtained via binary optimization over a discrete problem space (Erdem & Sclaroff, 2006). It can also be applied in security systems for industrial automation, traffic monitoring, and surveillance in public places, like museums, shopping malls, subway stations and parking lots, (Mittal & Davis, 2008; Mittal & Davis, 2004).

With visibility analysis and sensor planning in dynamic environments, in which the methods include computing occlusion-free viewpoints (Tarabanis et al., 1996) and feature detectability constraints (Tarabanis, Tsai & Allen, 1994), applications are widely existing in product inspection, assembly, and design in reverse engineering (Yegnanarayanan, Umamaheswari & Lakshmi, 2009; Tarabanis et al, 1995b; Scott, 2009).

In other aspects, an approach was proposed in (Marchand, 2007) to control camera position and/or lighting conditions in an environment using image gradient information. Auto-focusing technique is used by (Quang, Kim & Lee, 2008) in a projector-camera system. Smart cameras are applied by (Madhuri, Nagesh, Thirumalaikumar, Varghese & Varun, 2009). Camera network is designed with dynamic programming by (Lim, Davis & Mittal, 2007).

4. Methods and Solutions

The early work on sensor planning was mainly focused on the analysis of placement constraints, such as resolution, focus, field of view, visibility, and conditions for light source placement in a 2D space. A viewpoint has to be placed in an acceptable space and a number of constraints should be satisfied. The fundamentals in solving such a problem were established in the last decades.

Here the review scope is restricted to some common methods and solutions found in recently published contributions regarding view-pose determination and sensor parameter setting in robotics. It does not include: foveal sensing, hand-eye coordination, autonomous vehicle control, landmark identification, qualitative navigation, path following operation, etc., although these are also issues concerning the active perception problem. We give little consideration to contributions on experimental study (Treuillet et al, 2007), sensor simulation (Loniot et al, 2007; Wu et al, 2005), interactive modeling (Popescu, Sacks & Bahmutov, 2004), and semi-automatic modeling (Liu & Heidrich, 2003) either.

For the methods and solutions listed below, they might be used independently, or as hybrids, in the above-mentioned applications and tasks.

4.1. Formulation of Constraints

An intended view must first satisfy some constraints, either due to the sensor itself, the robot, or its environment. From the work by Cowan et al who made a highlight on the sensor placement problem, detailed descriptions of the acceptable viewpoints for satisfying many requirements (sensing constraints) have to be provided. Tarabanis et al. presented approaches to compute the viewpoints that satisfy many sensing constraints, i.e. resolution, focus, field-of-view, and detectability (Tarabanis et al, 1996; Tarabanis et al, 1995b; Tarabanis et al, 1994). Abrams et al also proposed to compute the viewpoints that satisfy constraints of resolution, focus (depth of field), field-of-view, and detectability (Abrams et al, 1999).

A complete list of constraints is summarized and analyzed by (Chen & Li, 2004). An admissible viewpoint should satisfy as many as nine placement constraints, including the geometrical (G₁, G₂, G₆), optical (G₃, G₅, G₈), reconstructive (G₄, G₆), and environmental (G₉) constraints. These are listed in Table III. Fig. 10 intuitively illustrates several constraints (G₁, G₂, G₃, G₅, G₇). Considering the 6 points (A - F) on the object surface, it can be seen in the figure that only point A satisfies all the five constraints, while all other points violated one or more of the constraints.

TABLE III SENSOR PLACEMENT CONSTRAINTS (Chen & Li, 2004)

Satisfaction	Constraint
G₁	Visibility
G₂	Viewing angle
G₃	Field of view
G₄	Resolution constraint
G₅	In-focus or viewing distance
G₆	Overlap
G₇	Occlusion
G₈	Image contrast (affect (d, f, a) settings)
G₉	Kinematic reachability of sensor pose

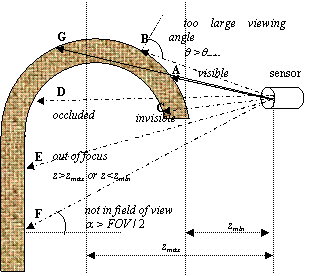
Fig. 10 Illustration of sensor placement constraints (Chen & Li, 2004)

The formulation of perception constraints is mostly used in model-based vision tasks (Trucco et al, 1997), such as inspection, assembly/disassembly, recognition, and object search (Tarabanis et al, 1995b), but the similar formulation is also valid in non-model based tasks (Chen et al, 2008a; Chen & Li, 2005). For the autonomous selection and modification of camera configurations during tasks, Chu and Chung consider both the camera's visibility and the manipulator's manipulability. The visibility constraint guarantees that the whole of a target object can be "viewed" with no occlusions by the surroundings, and the manipulability constraint guarantees avoidance of the singular position of the manipulator and rapid modification of the camera position. The optimal camera position is determined and the camera configuration is modified such that visual information for the target object can be obtained continuously during the execution of assigned tasks (Chu & Chung, 2002).

4.1.1. Cost Functions

Traditionally for sensor planning, a weighted function is often used for objective evaluation. It includes several components standing for placement constraints. For object model, the NBV was defined as the next sensor pose which would enable the greatest amount of previously unseen three-dimensional information to be acquired (Banta et al, 2000; Li & Liu, 2005). Tarabanis et al chose to formulate the probing strategy as a function minimization problem (Tarabanis et al, 1995b). The optimization function is given as a weighted sum of several component criteria, each of which characterizes the quality of the solution with respect to an associated requirement separately. The optimization function is written as:

(6)

subject to g_i³0, to satisfy four constraints, i.e. the resolution, focus, field-of-view, and visibility.

Equivalently with constraint-based space analysis, for each constraint, the sensor pose is limited to a possible region. Then the viewpoint space is given as the intersection of these regions and the optimization solution is determined by the above function in the viewpoint space, i.e.,

(7)

In (Marchand & Chaumette, 1999a), the strategy of viewpoint selection took into account three factors: (1) the new observed area volume G(f_t+1), (2) the cost function F in order to reduce the total camera displacement C(f_t, f_t+1), and (3) constraints to avoid unreachable viewpoints and to avoid positions near the robot joint limits B(f). The cost function F_next to be minimized is defined as a weighted sum of the different measures:

(8)

Ye and Tsotsos considered the total cost of object search via a function (Ye & Tsotsos, 1999):

(9)

where the cost t_o(f) gives the total time needed to manipulate the hardware to the status specified by f , to take a picture, to update the environment and register the space, and to run the recognition algorithm. The effort allocation F = (f₁, ..., f_k ) gives the ordered set of operations applied in the search.

Chen and Li defined a criterion of lowest traveling cost according to the task execution time

(10)

where T1 and T2 are constants reflecting the time for image digitalization, image preprocessing, 3D surface reconstruction, fusion and registration of partial models. n is the number of total viewpoints. k is the equivalent sensor moving speed. l_c is the total path length of robot operations, which is computed from the sensor placement graph (Chen & Li, 2004).

4.1.2. Data-Driven

In active perception, data-driven sensor planning is to make sensing decisions according to local on-site data characteristics and to deal with environmental uncertainty (Miura & Ikeuchi, 1998; Miura & Ikeuchi, 1998; Whaite & Ferrie, 1997; Callari & Ferrie, 2001; Bodor et al, 2007).

In model-based object recognition, SyedaMahmood presents an approach that uses color as a cue to perform selection either based solely on image-data (data-driven), or based on the knowledge of the color description of the model (model-driven). The color regions extracted form the basis for performing data and model-driven selection. Data-driven selection is achieved by selecting salient color regions as judged by a color-saliency measure that emphasizes attributes that are also important in human color perception. The approach to model-driven selection, on the other hand, exploits the color and other regional information in the 3D model object to locate instances of the object in a given image. The approach presented tolerates some of the problems of occlusion, pose and illumination changes that make a model instance in an image appear different from its original description (SyedaMahmood, 1997).

Mitsunaga and Asada investigated how a mobile robot selected landmarks to make a decision based on an information criterion. They argue that observation strategies should not only be for self-localization but also for decision making. An observation strategy is proposed to enable a robot equipped with a limited viewing angle camera to make decisions without self-localization. A robot can make a decision based on a decision tree and on prediction trees of observations constructed from its experiences (Mitsunaga & Asada, 2006).

4.2. Expectation

Local surface features and expected model parameters are often used in active sensor planning for shape modeling (Flandin & Chaumette, 2001). A strategy developed by Jonnalagadda et al. is to select viewpoints in four steps: local surface feature extraction, shape classification, viewpoint selection and global reconstruction. When 2D and 3D surface features are extracted from the scene, they are assembled into simple geometric primitives. The primitives are then classified into shapes, which are used to hypothesize the global shape of the object and plan next viewpoints (Jonnalagadda et al, 2003).

In purposive shape reconstruction, the method adopted by Kutulakos and Dyer is based on a relation between the geometries of a surface in a scene and its occluding contour: If the viewing direction of the observer is along a principal direction for a surface point whose projection is on the contour, surface shape (i.e., curvature) at the surface point can be recovered from the contour. They use an observer that purposefully changes viewpoint in order to achieve a well-defined geometric relationship with respect to a 3D shape prior to its recognition. The strategy depends on only curvature measurements on the occluding contour (Kutulakos & Dyer, 1994).

Chen and Li developed a method by analyzing the target's trend surface, which is the regional feature of a surface for describing the global tendency of change. While previous approaches to trend analysis usually focused on generating polynomial equations for interpreting regression surfaces in three dimensions, they propose a new mathematical model for predicting the unknown area of the object surface. A uniform surface model is established by analyzing the surface curvatures. Furthermore, a criterion is defined to determine the exploration direction, and an algorithm is developed for determining the parameters of the next view (Chen & Li, 2005).

On the other hand, object recognition does also obviously need to analyze local surface features. The appearance of an object from various viewpoints is described in terms of visible 2D features, which are used for feature search and viewpoint decision (Kuno et al, 1991).

4.2.1. Visibility

A target of feature point must be visible and not occluded in a robotic vision system (Briggs & Donald, 2000; Chu & Chung, 2002). It is essential for real-time robot manipulation in cluttered environments (Zussman et al, 1994; Jang et al, 2008), or adaptation to dynamic scenes (Fiore et al, 2008). Recognition of time-varying geometrical objects or subjects needs to maximize the visibility in dynamic environment (Mackay & Benhabib, 2008b).

As some missing areas may be found from the initial scans of an object (Fernandez et al, 2008), algorithms can be developed to compute additional scanning orientations (Chang & Park, 2009). The algorithm by Chang and Park was designed by considering three major technological requirements of the problem: dual visibility, reliability, and efficiency. To satisfy the dual visibility requirement for the structured light vision sensor, the algorithm uses the concept of a visibility map as well as the diameter of a spherical polygon. Once dual visibility is satisfied, the algorithm attempts to locate the optimal scanning orientation to maximize the reliability. For a surface, the visibility map can be derived from a Gauss map, which is the intersection of the surface normal vectors and the unit sphere (Fig. 11).

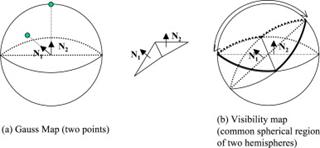
Fig. 11 The Gauss map and visibility map for scanning planning (Chang & Park, 2009)

Model-based visibility measure for geometric primitives called visibility map. It is simple to calculate, memory efficient, accurate for viewpoints outside the convex hull of the object and versatile in terms of possible applications (Ellenrieder, Kruger, Stossel & Hanheide, 2005). A global visibility map is a spherical image built to describe the complete set of global visible view directions for a surface. In (Liu, Liu & Ramani, 2009), for computation of global visibility maps, both the self-occlusions introduced by a region and the global occlusions introduced by the rest of the surfaces on the boundary of the polyhedron are considered. The occluded view directions introduced between a pair of polyhedral surfaces can be computed from the spherical projection of the Minkowski sum of one surface and the reflection of the other. A suitable subset of the Minkowski sum, which shares the identical spherical projection with the complete Minkowski sum, is constructed to obtain the spherical images representing global occlusions (Liu et al, 2009).

4.2.2. Coverage, Occlusion, Tessellation

The sensor coverage problem for locating sensors in 2D can be modeled as an Art Gallery problem or museum problem (Bottino & Laurentini, 2006b; Bottino, Laurentini & Rosano, 2007; Bottino & Laurentini, 2008). It originates from a real-world problem of guarding an art gallery with the minimum number of guards which together can observe the whole gallery. In the computational geometry, the layout of the art gallery is represented by a simple polygon and each guard is represented by a point in the polygon. A set S of points is said to guard a polygon if, for every point p in the polygon, there is some q Î S such that the line segment between p and q does not leave the polygon.

The decision problem versions of the art gallery problem and all of its standard variations are NP-complete. Regarding approximation algorithms, Eidenbenz et al. proved the problem to be APX-hard, implying that it is unlikely that any approximation ratio better than some fixed constant can be achieved by a polynomial time approximation algorithm. Avis and Toussaint proved that a placement for these guards may be computed in O(n log n) time in the worst case, via a divide and conquer algorithm.

Recently, Nilsson et al. formulated the “minimum wall guard problem” as

Problem: Let W = [(p_i, q_i): p_i, q_i ∈ R²] be a set of line segments corresponding to the walls that needs to be surveyed. Furthermore, let O Ì R² be the union of all obstacles. The problem is to find a minimum set S Ì R² of points on the ground plane such that every wall w_i in W is guarded by a point s_j in S. By guarded it means that s_j and w_i satisfy the constraints of visibility, resolution, and field of view.

They further propose the following algorithm to find a solution.

Algorithm: (1) Find the candidate guard set S; (2) Calculate the walls guarded by each s ∈S, using the three constraints; (3) Transcribe the problem of finding a subset of S that guards all walls W to a minimum set cover problem; (4) Solve the problem using a greedy approach.

In the algorithm, since the original problem is NP-complete, they do not seek to find the true optimal set of guard positions. Instead, a near optimal subset of the candidate points is chosen with a known approximation ratio of O(log(n)) (Nilsson et al, 2009).

As the Art Gallery problem is a well-studied visibility problem in computational geometry, many other solutions may be taken directly for visual sensor placement. Recently, a lower bound for the cardinality of the optimal covering solution, specific of a given polygon, has been proposed. It allows one to assess the performances of approximate sensor location algorithms. It can be computed in reasonable time for environments with up to a few hundreds of edges (Bottino et al, 2009).

An example of complex scenario is depicted in Fig. 12. Seven UGVs are required to cover the 19 walls of the four buildings. Note that although no explicit obstacles are present, the buildings themselves serve as obstacles occluding the view of the UGVs.

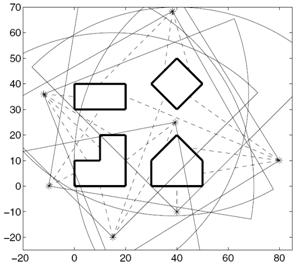
Fig. 12 A complex scenario with 19 walls to be guarded. The solution requires seven guards to guard all walls while satisfying occlusion, resolution and field of view constraints (Nilsson et al, 2009).

However, if the problem is in 3D, then putting a guard at each vertex will not ensure that all of the museums are under observation. Although all of the surface of the polyhedron would be surveyed, for some polyhedra there are points in the interior which might not be under surveillance.

To determine minimal orthographic view covers for polyhedra, a global visibility map based method is developed in (Liu & Ramani, 2009) to calculate an optimal or near-optimal solution using object space segmentation and viewpoint space sampling. The viewpoint space is sampled using a generate-as-required heuristic. The problem is then modeled as an instance of the classical set-cover problem and solved using a minimal visible set based branch-and-bound algorithm.

Coverage is also a cue in image selection for multi-view 3D sensing (Hornung et al, 2008), urban driving (Seo & Urmson, 2008), multi-agent sensor planning (Bardon et al, 2004), and model acquisition session planning. Impoco et al. propose a solution to improve the coverage of automatically acquired objects. Rather than searching for the NBV in order to minimize the number of acquisitions, they propose a simple and easy-to-implement algorithm limiting our scope to closing gaps (i.e. filling unsampled regions) in roughly acquired models. The idea is to detect holes in the current model and cluster their estimated normals in order to determine new views (Impoco, Cignoni & Scopigno, 2004).

While most existing camera placement algorithms focus on coverage and/or visibility analysis, Yao et al. recently argued that visibility is insufficient for automated persistent surveillance. In some applications, a continuous and consistently labeled trajectory of the same object should be maintained across different camera views. Therefore, a sufficient uniform overlap between the cameras' FOVs should be secured so that camera handoff can successfully and automatically be executed before the object of interest becomes untraceable or unidentifiable. They propose sensor-planning methods that improve existing algorithms by adding handoff rate analysis and preserve necessary uniform overlapped FOVs between adjacent cameras for an optimal balance between coverage and handoff success rate (Yao et al, 2010; Lim et al, 2006).

There is a constraint in sensor planning that has not been thoroughly investigated in the literature, namely, visibility in the presence of random occluding objects (Mittal & Davis, 2008; Mittal & Davis, 2004). Such visibility analysis provides important performance characterization of multi-camera systems. Furthermore, maximization of visibility in a given region of interest yields the optimum number and placement of cameras in the scene. Mittal and Davis presented such primary contributions.

Although several factors contribute, occlusion due to moving objects within the scene itself is often the dominant source of tracking error. Chen and Davis introduced a configuration quality metric based on the likelihood of dynamic occlusion. Since the exact geometry of occluders can not be known a priori, they use a probabilistic model of occlusion (Chen & Davis, 2008).

There is another distinctive method used frequently for object modeling, i.e. spatial tessellation. Usually it tessellates a sphere or cylinder around the object to be modeled as a viewpoint space (MacKinnon et al, 2008a), look-up array, or grid maps (Se & Jasiobedzki, 2007). Each grid point is a possible sensor pose for viewing the object. The object surface is partitioned as void surface, seen surface, unknown surface, and uncertain surface. The working space is also partitioned into void volume and viewing volume. Finally an algorithm is employed for planning a sequence of viewpoints so that the whole object can be sampled. This method is effective in dealing with some small and simple objects, but it is difficult to model a large and complex object with many concave areas because it cannot solve occlusion constraint.

4.2.3. Geometrical Analysis

Direct geometrical analysis is the most fundamental way in solving computer vision problems. For example, the robot configuration space, C-space, is adopted with pure geometric criteria (Wang & Gupta, 2006). For simultaneous tracking of multiple moving targets using an active stereo, Barreto et al. propose to control the active system parameters in such a manner that the images of the targets in the two views are related by a homography. This homography is specified during the design stage and, thus, can be used to implicitly encode the desired tracking behavior. Such formulation leads to an elegant geometric framework that enables a systematic and thorough analysis of the problem. In the case of using two pan-tilt-zoom (PTZ) cameras with rotation and zoom control, it is proved that such a system can track up to three free-moving targets, while assuring that the image location of each target is the same for both views. If considering a robot head with neck pan motion and independent eye rotation, it is not possible to track more than two targets because of the lack of zoom (Barreto et al, 2010).

For optimal sensor placement in a surveillance region with a minimal cost, the problem is solved by Sivaram et al. by obtaining a performance vector, with its elements representing the performances of subtasks, for a given input combination of sensors and their placement. Then the optimal sensor selection problem can be converted into the form of Integer Linear Programming problem. The optimal performance vector corresponding to the sensor combination n (m-dimensional) is given by

P* = A ´ n (11)

where A is related to the performance matrix (l´m) which is organized from the sensor types and surveillance subtasks. The performance constraints can be written as

A ´ n ³ b (12)

where b is the required performance, an l-dimensional vector. To demonstrate the utility of our technique, a surveillance system is introduced which consists of PTZ cameras and active motion sensors for capturing faces (Sivaram et al, 2009).

In a robot motion planning algorithm, Han et al. proposed to capture a moving object precisely using the single curvature trajectory. With the pre-determined initial states (i.e., position and orientation of the mobile robot and the final states), the mobile robot is made to capture a moving object (Han et al, 2008).

4.2.4. Volumetric Space

Out of existing approaches, volumetric computation by region intersection is frequently used by researchers since the early stage (Cowan & Kovesi, 1988). For example, it computes the region R_i of acceptable viewpoints for each constraint. If multiple surface features need to be inspected simultaneously, the region R_i is the intersection of the acceptable regions R_ij for each individual feature. Finally, the region of acceptable viewpoints is the intersection of all regions (Fig. 13).

Fig. 13 The volumes of resolution, depth-of-field, and field-of-view constraints (Cowan & Kovesi, 1988)

For scene reconstruction and exploration (Lang & Jenkin, 2000), the quality of a new position f_i+1 is defined by the volume of the unknown regions that appear in the field of view of the camera (Marchand & Chaumette, 1999a). The new observed region G(f_i+1) is given by:

G(f_i+1) = V(f_i+1) - V(f_i+1)ÇV(T₀^t) (13)

where V(f_i+1) defines the part of the scene observed from the position f_i+1 and V(f_i+1)ÇV(T₀^t) defines the subpart of V(f_i+1) that has been already observed.

Martins et al. presented a method to automate the process of surface scanning using optical range sensors and based on a priori known information from a CAD model. A volumetric model implemented through a 3D voxel map is generated from the object CAD model and used to define a sensing plan composed of a set of viewpoints and the respective scanning trajectories. Surface coverage with high data quality and scanning costs are the main issues in sensing plan definition (Martins et al, 2005; Martins et al, 2003).

Bottino and Laurentini presented a general approach to interactive, object-specific volumetric algorithms, based on a condition for the best possible reconstruction. The approach can be applied to any class of objects. As an example, an interactive algorithm is implemented for convex polyhedra (Bottino & Laurentini, 2006a).

4.3. Multi-agent Approach

4.3.1. Cooperative Network

Consider a mobile cooperative network that is given the task of building a map of the spatial variations of a parameter of interest, such as an obstacle map or an aerial map. Mostofi and Sen proposed a framework that allows the nodes to build a map with a small number of measurements. By compressive sensing, they studied how the nodes can exploit the sparse representation in the transform domain in order to build a map with minimal sensing (Mostofi & Sen, 2009).

The surveillance of a manoeuvring target with multiple sensors in a coordinated manner requires a method for selecting and positioning groups of sensors in real time (Naish, Croft & Benhabib, 2003). Heuristic rules are used to determine the composition of each sensor group by evaluating the potential contribution of each sensor. In the case of dynamic sensors, the position of each sensor with respect to the target is specified. The approach aims to improve the quality of the surveillance data in three ways: (1) The assigned sensors are manoeuvred into "optimal" sensing positions, (2) the uncertainty of the measured data is mitigated through sensor fusion, and (3) the poses of the unassigned sensors are adjusted to ensure that the surveillance system can react to future object manoeuvres. If a priori target trajectory information is available, the system performance may be further improved by optimizing the initial pose of each sensor off-line.

As a single sensor system would not provide adequate information for a given sensor task, it is necessary to incorporate multiple sensors in order to obtain complete information. Hodge and Kamel presented an automated system for multiple sensor placement based on the coordinated decisions of independent, intelligent agents. The overall goal is to provide the surface coverage necessary to perform feature inspection on one or more target objects in a cluttered scene. This is accomplished by a group of cooperating intelligent sensors. In the system, the sensors are mobile, the target objects are stationary and each agent controls the position of a sensor and has the ability to communicate with other agents in the environment. By communicating desires and intentions, each agent develops a mental model of the other agents' preferences, which is used to avoid or resolve conflict situations (Hodge & Kamel, 2003).

Bakhtari et al. developed another agent-based method for the dynamic coordinated selection and positioning of active-vision cameras for the simultaneous surveillance of multiple objects as they travel through a cluttered environment with unknown trajectories. The system dynamically adjusts the camera poses in order to maximize the system's performance by avoiding occlusions and acquiring images with preferred viewing angles (Bakhtari & Benhabib, 2007; Bakhtari et al, 2006).

In other aspects, camera networking by dynamic programming is addressed in (Lim et al, 2007). Issues of scalability and flexibility of multiple sensors are studied in (Hodge, Kamel & Bardon, 2004). Cooperative localization using relative bearing constraints is used for error analysis in (Taylor & Spletzer, 2007).

4.3.2. Fusion

When multiple optical sensors like stereo vision, laser-range scanner and laser-stripe profiler are integrated into a multi-purpose vision system, fusion of range data into a consistent representation is necessary to allow for safe path planning and view planning. Suppa and Hirzinger dealt with such 3D sensor synchronization and model generation (Suppa & Hirzinger, 2007). Cohen and Edan presented a sensor fusion framework for selecting online the most reliable logical sensors and the most suitable algorithm for fusing sensor data in a robot platform (Cohen & Edan, 2008).

Visual sensors provide exclusively uncertain and partial knowledge of a scene. A suitable scene knowledge representation is useful to make integration and fusion of new, uncertain and partial sensor measures possible. Flandin and Chaumette develop a method based on a mixture of stochastic and set membership models. Their approximated representation mainly results in ellipsoidal calculus by means of a normal assumption for stochastic laws and ellipsoidal over or inner bounding for uniform laws. These approximations allow us to build an efficient estimation process integrating visual data on line. Based on this estimation scheme, optimal exploratory motions of the camera can be automatically determined (Flandin & Chaumette, 2002).

While wide-area video surveillance is an important application, it is sometimes not practical to have video cameras that completely cover the entire region of interest. For obtaining good surveillance results in a sparse camera networks, it requires that they be complemented by additional sensors with different modalities, their intelligent assignment in a dynamic environment, and scene understanding using these multimodal inputs. Nayak et al. propose a probabilistic scheme for opportunistically deploying cameras to the most interesting parts of a scene dynamically given data from a set of video and audio sensors. Events are tracked continuously by combining the audio and video data. Correspondences between the audio and video sensor observations are obtained through a learned homography between the image plane and ground plane (Nayak et al, 2008; Bakhtari et al, 2006).

For 3D Tracking, Chen and Li propose a method to fuse sensing data of the most current observation into a 3D visual tracker with particle techniques. The importance density function in particle filter can be modified to represent posterior states by particle crowds in a better way. Thus, it makes the tracking system more robust to noise and outliers (Chen & Li, 2008).

For vehicle localization, data fusion from GPS and machine vision is proposed in (Rae & Basir, 2009). Data association is needed to identity the detected objects, and to identity the road driven by the vehicle. For this purpose they employ Multiple Hypothesis Tracking to consider multiple data association hypotheses simultaneously. Results show that using machine vision improves the localization accuracy and helps the identification of the road being driven by the vehicle.

4.4. Statistical Approaches

4.4.1. Probability and Entropy

Statistics, probability, Kalman filter, and associative Markov networks have been widely used in active object recognition (Wheeler & Ikeuchi, 1995; Roy et al, 2000; Dickinson et al, 1997; Caglioti, 2001), grasping (Motai & Kosaka, 2008), and modeling (Triebel & Burgard, 2008). In the research of multi-camera solutions, Farshidi et al investigated the feasibilities of recognition algorithms to classify the object if its pose can be determined with a high confidence level, by processing the available information within a recursive Bayesian framework at each step. Otherwise, the algorithms compute the next most informative camera positions for capturing more images. The principle component analysis (PCA) is used to produce a measurement vector based on the acquired images. Occlusions in the images are handled by a probabilistic modelling approach that can increase the robustness of the recognition process with respect to structured noise. The camera positions at each recognition step are selected based on two statistical metrics regarding the quality of the observations, namely the mutual information (MI) and the Cramer-Rao lower bound (CRLB) (Farshidi et al, 2009). For the state sⁿ being the variable of interest, the MI is a measure of the reduction in the uncertainty in sⁿ due to the observation g and is defined as

I(sⁿ; g | a_n) = H(sⁿ | a_n) - H(sⁿ |g , a_n) (14)

where a_n is the vector of camera positions, g is the observation vector, and H() is the entropy function defined in (16). CRLB is computed by

(15)

where J_n is the Fisher information matrix.

Significant improvement is observed in the success rates of both MI-based and CRLB-based approaches. This enhancement was gained by incorporating a model of occlusion into the algorithms. The recognition rate in experiments without occlusion modeling is 48-50%, and improved to 98% if with occlusion modeling.

Borotschnig et al. also presented an active vision system for recognizing objects which are ambiguous from certain viewpoints (Borotschnig & Paletta, 2000). The system repositions the camera to capture additional views and uses probabilistic object classifications to perform view planning. Multiple observations lead to a significant increase in recognition rate. The view planning consists in attributing a score to each possible movement of the camera. The movement obtaining the highest score will be selected next. It was based on the expected reduction in Shannon entropy over object hypotheses given a new viewpoint, which should consist in attributing a score s_n(Dψ) to each possible movement Dψ of the camera. The movement obtaining the highest score will be selected next:

Dψ_n+1 := arg max s_n(Dψ) (16)

In sensor planning for object search, each robot action is defined by a viewpoint, a viewing direction, a field-of-view, and the application of a recognition algorithm. Ye and Tsotsos formulate it as an optimization problem: the goal is to maximize the probability of detecting the target with minimum cost. Since this problem is proved to be NP-Complete, in order to efficiently determine the sensing actions over time, the huge space of possible actions with fixed camera position is decomposed into a finite set of actions that must be considered. The next action is then selected from among these by comparing the likelihood of detection and the cost of each action. When detection is unlikely at the current position, the robot is moved to another position where the probability of target detection is the highest (Ye & Tsotsos, 1999).

The Shannon entropy was also applied to the problem of automatic selection of light positions in order to automatically place light sources for maximum visual information recovery (Vazquez, 2007).

The 3D site modeling in (Wenhardt, Deutsch, Angelopoulou & Niemann, 2007) is based on a probabilistic state estimation with sensor actions. The next best view is determined by a metric of the state estimation's uncertainty. Three metrics are addressed: D-optimality, which is based on the entropy and corresponds to the determinant of the covariance matrix of a Gaussian distribution, E-optimality, and T-optimality, which are based on eigenvalues or on the trace of matrices, respectively.

The entropy H(q) of a probability distribution p(q) is defined as (Li & Liu, 2005; Farshidi et al, 2009)

(17)

For an n-dimensional Gaussian distribution, the entropy can be calculated in a closed form:

(18)

The entropy depends only on the covariance P and the expected covariance is independent of next observations. This allows us to use the entropy as an optimality criterion for sensor planning (Wenhardt et al, 2007).

For sensor-based robot motion planning, the robot plans the next sensing action to maximally reduce the expected C-space entropy, called the Maximal expected Entropy Reduction (MER) criterion. From a C-space perspective, MER criterion consists of two important aspects: sensing actions are evaluated in C-space (geometric aspect); these effects are evaluated in an information theoretical sense (stochastic aspect). Wang and Gupta investigate how much of the performance is attributable to the paradigmatic shift to evaluating the sensor action in C-space and how much to the stochastic aspect, respectively (Wang & Gupta, 2006).

In an intelligent and efficient strategy for unstructured environment sensing using mobile robot agents, a metric is derived from Shannon's information theory to determine optimal sensing poses (Sujan & Meggiolaro, 2005). The map is distributed among the agents using an information-based relevant data reduction scheme. The method is particularly well suited to unstructured environments, where sensor uncertainty is significant. In their other contributions for site modeling and exploration, besides using Shannon's information theory to determine optimal sensing poses, the quality of the information in the model is used to determine the constraint-based optimum view for task execution. The algorithms are applicable for both an individual agent as well as multiple cooperating agents (Sujan & Dubowsky, 2005b). The NBV is found by fusing a Kalman filter in the statistical uncertainty model with the measured environment map (Sujan & Dubowsky, 2005a).

4.4.2. Bayesian Reasoning

Bayesian reasoning and classification methods are used in active perception for object recognition, search, surface reconstruction, and object modeling (Carrasco & Mery, 2007; Mason, 1997). Sutton and Stark also applied function-based reasoning for goal-oriented image segmentation (Sutton & Stark, 2008) and Zhang et al. proposed a Bayesian network approach to sensor modeling and path planning (Zhang et al, 2009).

Bayesian inference is statistical inference in which evidence or observations are used to update or to newly infer the probability that a hypothesis may be true. Bayes' theorem adjusts probabilities given new evidence in the following way:

(19)

where H represents a specific hypothesis, which may or may not be some null hypothesis. P(H) is called the prior probability of H that was inferred before new evidence, E, became available. P(E | H) is called the conditional probability of seeing the evidence E if the hypothesis H happens to be true. It is also called a likelihood function when it is considered as a function of H for fixed E. P(E) is called the marginal probability of E: the a priori probability of witnessing the new evidence E under all possible hypotheses.

For active recognition, the probability distribution of object appearance is described by multivariate mixtures of Gaussians which allows the representation of arbitrary object hypotheses (Eidenberger et al, 2008). In a statistical framework, Bayesian state estimation updates the current state probability distribution based on a scene observation which depends on the sensor parameters. These are selected in a decision process which aims at reducing the uncertainty in the state distribution (Eidenberger et al, 2008). For online recognition and pose estimation of a large isolated 3D object, Roy et al. propose a probabilistic reasoning framework for recognition and next-view planning (Roy et al, 2005).

Kristensen et al. proposed the sensor planning approach using the Bayesian decision theory. The sensor modalities, tasks, and modules were described separately and the Bayes decision rule was used to guide the behavior (Kristensen, 1997). Li and Liu adopted a B-spline for modeling the freeform surface. In the framework of Bayesian statistics for determining the probing points for efficient measurement and reconstruction, they develop a model selection strategy to obtain an optimal model structure for the freeform surface. In order to obtain reliable parameter estimation for the B-spline model, they analyzed the uncertainty of the model and used the statistical analysis of the Fisher information matrix to optimize the locations of the probing points needed in the measurements (Li & Liu, 2003).

4.4.3. Hypothesis and Verification

The way following “observation, modeling, hypothesis and verification” is powerful for 3D model matching. In a semi-automated excavation system, the 3D object localization method used consists of three steps (Maruyama et al, 2010). (1) Candidate regions are extracted from a range image obtained by an area-based stereo-matching method. (2) For each region, multiple hypotheses for the position and orientation are generated for each object model. (3) Each hypothesis is verified and improved by an iterative method. The operator verifies the object localization results and then selects one of the objects as the best object that is suitable for grasping by the robot. The robot grasps objects based on the object localization result (Maruyama et al, 2010).

For path planning, a strategy by (Nabbe & Hebert, 2007) is based on a "what-if" analysis of hypothetical future configurations of the environment. Candidate sensing positions are evaluated based on their ability to observe anticipated obstacles.

Hypothesis and verification is also used in viewpoint planning for 3D model reconstruction in (Jonnalagadda et al, 2003) and (Marchand & Chaumette, 1999b). Jonnalagadda et al. presented a strategy to select viewpoints for global 3D reconstruction of unknown objects. The NBV is chosen to verify the hypothesized shape. If the hypothesis is verified, some information about global reconstruction of a model can be stored. If not, the data leading up to this viewpoint is re-examined to create a more consistent hypothesis for the object shape. The NBV algorithm uses only the local geometric features of an object and the visibility constraint is not used in the function to compute next viewpoint (Jonnalagadda et al., 2003).

To perform the complete and accurate reconstruction of 3D static scenes, Marchand and Chaumette used a structure from controlled motion method. As the method is based on particular camera motions, perceptual strategies able to appropriately perform a succession of such individual primitive reconstructions are proposed in order to recover the complete spatial structure of the scene. Two algorithms are suggested to ensure the exploration of the scene. The former is an incremental reconstruction algorithm based on the use of a prediction/verification scheme managed using decision theory and Bayes nets. It allows the visual system to get a high level description of the observed part of the scene. The latter, based on the computation of new viewpoints ensures the complete reconstruction of the scene (Marchand & Chaumette, 1999b).

4.5. Soft and Intelligent Computation

4.5.1. Learning and Expert System

Interactive learning (Grewe & Kak, 1995) or reinforcement learning (Kollar & Roy, 2008) is frequently used for active recognition, localization, planning, and modeling (Wang et al, 2008). For example, inter-image statistics can be used for 3D environment modeling (Torres-Mendez & Dudek, 2008). An expert knowledge based sensor planning system was developed for car headlight lens inspection by (Martinez et al, 2008).

For active viewpoint selection for object recognition, Deinzer et al. attempted an unsupervised reinforcement learning algorithm for modeling of continuous states, continuous actions, sequential fusion of gathered image information, and supporting rewards for an optimized recognition. The combined viewpoint selection and viewpoint fusion approach is to improve the recognition rates (Deinzer et al, 2009). Roy et al. attempted probabilistic reasoning for recognition of an isolated 3D object. Both the probability calculations and the next view planning have the advantage that the knowledge representation scheme encodes feature-based information about objects as well as the uncertainty in the recognition process. The probability of a class (a set of aspects, equivalent with respect to a feature set) was obtained from the Bayes rule (Roy et al, 2000).

For robotic real-time localization with a single camera and natural landmarks, Kwok employed an evolutionary computing approach (Kwok 2006) in the SLAM context to build a map simultaneously. Royer et al. gave a three-step approach. In a learning step, the robot is manually guided on a path and a video sequence is recorded with a front looking camera. Then a structure from motion algorithm is used to build a 3D map from this learning sequence. Finally in the navigation step, the robot uses this map to compute its localization in real-time and it follows the learning path or a slightly different path if desired (Royer et al., 2007).

Consider the task of purposefully controlling the motion of an active, monocular observer in order to recover a global description of a smooth, arbitrarily-shaped object. Kutulakos and Dyer formulate global surface reconstruction as the task of controlling the motion of the observer so that the visible rim slides over the maximal, connected, reconstructible surface regions intersecting the visible rim at the initial viewpoint. They develop basic strategies that allow reconstruction of a surface region around any point in a reconstructible surface region. These strategies control viewpoint to achieve and maintain a well-defined geometric relationship with the object's surface, rely only on information extracted directly from images, and are simple enough to be performed in real time. Global surface reconstruction is then achieved by (1) appropriately integrating these strategies to iteratively grow the reconstructed regions, and (2) obeying four simple rules (Kutulakos & Dyer, 1995).

Robots often use topological structures as a spatial representation for exploring unknown environments. A method is developed in (Hubner & Mallot, 2007) to scale a similarity based navigation system (the view-graph-model) to continuous metric localization. Instead of changing the landmark model, they embed the graph into the 3D pose space. Therefore, recalibration of the path integrator is only possible at discrete locations in the environment. The navigation behavior of the robot is controlled by a homing algorithm which combines three local navigation capabilities, obstacle avoidance, path integration, and scene based homing. This homing scheme allows automated adaptation to the environment. It is further used to compensate for path integration errors, and therefore allows a robot to derive globally consistent pose estimates based on weak metric knowledge. It is tested to explore a large, open, and cluttered environment.

Rule-based planning. Semantic maps and reasoning engines are useful in addition to geometry map because it becomes inevitable if the robot interacts with its environment in a goal-directed way. A semantic stance enables the robot to reason about objects; it helps disambiguate or round off sensor data; and the robot knowledge becomes reviewable and communicable. Nüchter and Hertzberg proposed an approach and an integrated robot system for semantic mapping. Coarse scene features are determined by semantic labeling. More delicate objects are then detected by a trained classifier and localized. Finally, the semantic maps can be visualized for inspection (Nüchter & Hertzberg, 2008). Fig. 14 shows an example of the object relationship for scene interpretation. The semantic mapping is done by the following steps: (1) SLAM for acquiring 3D scans of the environment; (2) Scene interpretation by feature extracting and labeling; (3) Object detection for identification of known objects and their poses; and (4) Visualization of the semantic map.

Fig. 14 Example of the constraint network with semantic mapping for scene interpretation (Nüchter & Hertzberg, 2008)

4.5.2. Fuzzy and Neural Network

Fuzzy inference and neural network are useful in sensor planning for prediction and recognition. Saadatseresht et al. solved automatic camera placement in vision metrology based on a fuzzy inference system (Saadatseresht, Samadzadegan & Azizi, 2005). Martinez et al. recently proposed a methodology to include the inspection guideline in an automated headlamp lens inspection system. As the way in which the guideline includes the knowledge of an expert in the inspection of lenses is inherently qualitative and vague, a Fuzzy Rule-Based System is developed to model this information (Martinez et al, 2009). Budiharto et al. used an adaptive neuro fuzzy controller for servant robot’s indoor navigation (Budiharto et al, 2010).

Visibility uncertainty prediction was solved by an artificial neural network (ANN) in (Saadatseresht & Varshosaz, 2007). For outdoor navigation, Shinzato et al. used ANN for path recognition (Shinzato et al, 2010).

4.5.3. Evolutionary Computation

The model-based sensor placement problem has been formulated as a nonlinear multi-constraint optimization problem as described in Subsection 4.2. It is difficult to compute robust viewpoints which satisfy all constraints. However, evolutionary computation is especially powerful in solving such problems. Chen and Li use a hierarchical genetic algorithm (GA) to determine the optimal topology in the sensor placements which will contain minimum number of viewpoints with the highest accuracy while satisfying all the constraints. In the hierarchical chromosome, parametric genes represent the sensor poses and optical settings and control genes represent the topology of viewpoints. A plan of sensor placements is evaluated by a min-max criterion, which includes three objectives and a fitness evaluation formula (Chen & Li, 2004). Similarly, a hybrid genetic algorithm is used to solve the highly complicated optimization problem in (Al-Hmouz & Challa, 2005).

Although evolutionary computation is mostly used in model-based inspection (Olague, 2002; Yang & Ciarallo, 2001; Dunn & Olague, 2004; Dunn & Olague, 2003), the method has wider applications of active vision perception, e.g., path planning in assembly lines (Park et al, 2006) and monitoring (Sakane et al, 1995). Kang et al. applied the virus coevolutionary partheno-genetic algorithm (VEPGA), which combined a partheno-genetic algorithm (PGA) with virus evolutionary theory, for determining sensor placements (Kang, Li & Xu, 2008).

4.6. Dynamic Configuration

In an active vision system, since the robot needs to move from one place to another for performing a multi-view task, a traditional vision sensor with fixed structure is often inadequate for the robot to perceive the object features in an uncertain environment as the object distance and size are unknown before the robot sees it. A dynamically reconfigurable sensor can help the robot to control the configuration and gaze at the object surfaces. For example, with a structured light system, the camera needs to see the object surface illuminated by the projector, to perform the 3D measurement and reconstruction task. Active recalibration means that the vision sensor is reconfigurable during runtime to fit in the environment and can perform self-recalibration in need before visual perception (Chen et al, 2008a; Chu & Chung, 2002).

In the literature, self reconfiguration of automated visual inspection systems is addressed in (Garcia & Villalobos, 2007a; Garcia & Villalobos, 2007b). Bakhtari et al. presented a reconfiguration method for the surveillance of an object as it travels through a multi-object dynamic workspace with unknown trajectory (Bakhtari et al, 2009; Bakhtari et al, 2006).

In the environment of large scenes having large depth ranges with depth discontinuities, it is necessary to aim cameras in different directions and to fixate at different objects. An active approach is suggested by coarse-to-fine image acquisition in (Das & Ahuja, 1996), which involves the following steps. (1) A new fixation point is selected from among the non-fixated, low-resolution scene parts of current fixation. (2) A reconfiguration of the cameras is initiated for re-fixation. As reconfiguration progresses, the images of the new fixation point is gradually deblured and the accuracy of the position estimate of the point improves allowing the cameras to be aimed at it with increasing precision. (3) The improved depth estimate is used to select focus settings of the cameras, thus completing fixation. Similarly, an active stereo head is implemented with visual behaviors by (Krotkov & Bajcsy, 1993), including functions of (1) aperture adjustment to vary depth of field and contrast, (2) focus ranging followed by fixation, (3) stereo ranging followed by focus ranging, and (4) focus ranging followed by disparity prediction followed by focus ranging.

4.6.1. Gaze and Attention

Gaze and attention are important functions for human to actively perceive in the environment, and so as for robots. Visual perceptual capability starts with an early vision process that exhibits changes in visual sensitivity such as night vision and flash blindness under changing scene illumination. Visual attention directs the limited gaze resource to resolve visual competition with the cooperation of top-down attention and conspicuous bottom-up guidance. Grounded in psychological studies, it has four factors, i.e. conspicuity, mental workload, expectation and capacity, which determine successful attention allocation. For purposive perception, many devices and systems have been invented for robotics (Dickinson et al, 1997).

Active gaze control allows us to overcome some of the limitations of using a monocular system with a relatively small field of view. To implement active gaze control in SLAM, a system was addressed by (Frintrop & Jensfelt, 2008b), which specializes in creating and maintaining a sparse set of landmarks based on a biologically motivated feature-selection strategy. A visual attention system detects salient features that are highly discriminative and ideal candidates for visual landmarks that are easy to redetect. It supports (1) the tracking of landmarks that enable a better pose estimation, (2) the exploration of regions without landmarks to obtain a better distribution of landmarks in the environment, and (3) the active redetection of landmarks to enable close loop. It is concluded that active camera control outperforms the passive approach (Frintrop & Jensfelt, 2008a).

Attention is often related to visual search. Consider the problem of visually finding an object in an unknown space. This is an optimization problem, i.e., optimizing the probability of finding the target given a fixed cost limit in terms of total number of robotic actions required to find the visual target. Shubina and Tsotsos present an approximate solution and investigate its performance and properties (Shubina & Tsotsos, 2010).

With a pre-determined sensor lens, it may be not able to deal with the scenes that have objects with different distances. Quang et al. presented a projector auto-focusing technique based on local blur information of the image that can overcome the above limitation. The algorithm is implemented on a projector-camera system, in order to focus the pattern which is projected by the projector on all objects in the scene sequentially. The proposed algorithm first obtains a blur-map of the scene on the image by using a robust local blur estimator, and then the region of interest is decided by thresholding the obtained blur-map. Since the main light source is provided by projector, the proposed auto-focusing algorithm achieves a good performance with different light conditions (Quang et al, 2008).

With the ego-motion (Shimizu et al, 2005), the robot is able to control the orientation of a single camera, while still allowing the robot to preview a wider area. In addition, controlling the orientation allows the robot to optimize its environment perception by only looking where the most useful information can be discovered (Radovnikovich et al, 2010).

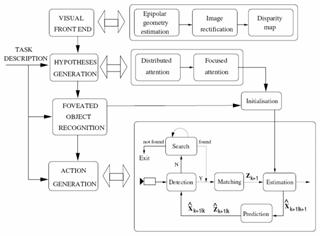
Fig. 15 The active vision system involving attention and gaze for action decision (Bjorkman & Kragic, 2004)

Bjorkman and Kragic introduced a real-time vision system that consists of two sets of binocular cameras: a peripheral set for disparity-based attention and a foveal one for higher-level processes (Fig. 15). Thus the conflicting requirements of a wide field of view and high resolution can be overcome. The steps taken from task specification through object recognition to pose estimation are completely automatic, combining both appearance and geometric models. It was tested in a realistic indoor environment with occlusions, clutter, changing lighting and background conditions (Bjorkman & Kragic, 2004).

4.6.2. Tagged Roadmap

Probabilistic roadmap methods are a class of randomized motion planning algorithms that have recently received considerable attention because they are capable of handling problems with many degrees of freedom, and large workspaces with many obstacles, for which other motion planning methods are computationally infeasible. Baumann et al. augments probabilistic road maps with vision-based constraints. The designed planner finds collision-free paths that simultaneously avoid occlusions of an image target and keep the target within the field of view of the camera (Baumann et al, 2008; Baumann et al, 2010).

Another probabilistic roadmap method is presented for planning the path of a robotic sensor deployed in order to classify multiple fixed targets located in an obstacle-populated workspace (Zhang et al, 2009). Existing roadmap methods are not directly applicable to robots whose primary objective is to gather target information with an on-board sensor. In the proposed information roadmap, obstacles, targets, sensor's platform and field-of-view are represented as closed and bounded subsets of a Euclidean workspace. The information roadmap is sampled from a normalized information theoretic function that favors samples with a high expected value of information in the configuration space. The method is applied to a landmine classification problem to plan the path of a robotic ground-penetrating radar, based on prior remote measurements and other geospatial data. Results show that paths obtained from the information roadmap exhibit classification efficiency several times higher than that of other existing search strategies. Also, the information roadmap can be used to deploy non-overpass capable robots that must avoid targets as well as obstacles (Zhang et al, 2009; Oniga & Nedevschi, 2010).

The research group of Allen et al. developed a system for automatic view planning called VuePlan. When combined with their mobile robot, AVENUE, the system is capable of modeling large-scale environments with minimal human intervention throughout both the planning and acquisition phases. The system proceeds in two distinct stages. In the initial phase, the system is given a 2D site footprint with which it plans a minimal set of sufficient and properly constrained covering views. It then uses a 3D laser scanner to take scans at each of these views. The planning system automatically computes and executes a tour of these viewing locations and acquires them with the robot's onboard laser scanner. These initial scans serve as an approximate 3D model of the site. The planning software then enters a second phase in which it updates this model by using a voxel-based occupancy procedure to plan the NBV (Blaer & Allen, 2009). They have successfully used the two-phase system to construct precise 3D models of real-world sites located in New York City (Fig. 16).

Fig. 16 Complex site modeling by view planning with a footprint (Blaer & Allen, 2009)

4.6.3. Solution for Next Best View

A solution for the next-best-view (NBV) problem is of particular importance for automated object modeling. Given a partial model of the target, we have to determine the sensor pose or scanning path to scan all the visible surfaces of an unknown object. The solution to this problem would ideally allow the model to be obtained from a minimum number of range images (Banta et al, 2000; Kim & Cho, 2003; Huang & Qian, 2008b; Huang & Qian, 2008a; Sun et al, 2008; He & Li, 2006b; Null & Sinzinger, 2006; Blaer & Allen, 2007).

The NBV may be computed in two steps. First, the exploration direction for the next view is determined via a mass vector chain based scheme. Then the accurate position of the next view is obtained by computing the boundary integral of the vectors fields. The position with the maximum integral value is selected as the NBV (He & Li, 2006a; Li et al, 2005; Chen & Li, 2005).

It is argued that solutions to the NBV problem are constrained by other steps in a surface acquisition system and by the range scanner's particular sampling physics. Another method for determining the unscanned areas of the viewing volume is presented in (Pito, 1999). The NBV is determined by maximizing the objective function N(i)

max N(i) = o(o_v(i), o_s(i)), iÎ[1, n]. (20)

where the parameters of o() are understood to be the confidence weighted area of void patch and partial model visible by the scanner. The number of costly computations needed to determine if an area of the viewing volume would be occluded from some scanning position is decoupled from the number of positions considered for the NBV, thus reducing the computational cost of choosing a viewpoint.

A self-termination criterion can be used for judging the completion condition in the measurement and reconstruction process. Li et al. derived such a condition based on changes in the volume computed from two successive viewpoints (He & Li, 2006a; Li et al, 2005).

4.6.4. Graph Based Placement

Graph theory played an important role in developing methods for automatic sensor placement (Yegnanarayanan et al, 2009; Sheng et al, 2001b; Kaminka et al, 2008). The general automatic sensor planning system (GASP) reported by Trucco et al is to compute optimal positions for inspection tasks using feature-based object models (Trucco et al, 1997). This exploits a feature inspection representation which outputs an explicit solution off-line for the sensor position problem. The viewpoints are planned by computing the visibility and reliability. In order to find a shortest path through the viewpoints in space, they used the convex hull, cheapest insertion, angle selection, or-optimization (CCAO) as the algorithm to solve the traveling salesman problem in the constructed graph (Fig. 17).

The method was further explicitly described by Chen and Li (Chen & Li, 2004), who gave detailed definition of the sensor placement graph and the traveling cost standard (Wang et al, 2007). A plan of viewpoints is mapped onto a graph with weight w on every edge E, where the vertices V_i represent viewpoints. Edge E_ij represents a shortest collision-free path between viewpoint V_i and V_j, and weight w_ij represents the corresponding distance. Fig. 18 shows an example topology of a viewpoint plan. A practical solution to sensor placement problem provides a number of viewpoints reachable by the robot and there must exist a collision free path between every two acceptable viewpoints.

Eggert attempted the use of the aspect graph for 3D object recognition (Eggert et al, 1995). The basic idea is that an iterative solution is generated for each of a set of candidate aspects and the best of these is chosen as the recognized view. Two assumptions are required: (1) the iterative search for the correct candidate aspect must converge to the correct answer, and (2) the solution found for the correct aspect muse be better than that found for any of the incorrect candidate aspects. In order to explore the validity of these assumptions, a simple aspect graph-based recognition system was implemented. The general definition of the aspect graph is that it is a graph structure in which: (1) there is a node for each general view of the object as seen from some maximal connected cell of viewpoint space, and (2) there is an arc for each possible transition across the boundary between the cells of two neighboring general views, called an accidental view or a visual event (Fig. 19).

In another way of object recognition by (Kuno et al, 1991), features are ranked according to the number of viewpoints from which they are visible. The rank and feature extraction cost of each feature are used to generate a tree-like strategy graph. This graph gives an efficient feature search order when the viewpoint is unknown, starting with commonly occurring features and ending with features specific to a certain viewpoint. The system searches for features in the order indicated by the graph. After detection, the system compares a line representation generated from the 3D model with the image features to localize the object.

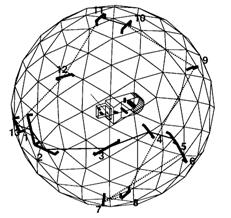
Fig. 17 The shortest path planned to take a stereo pair through the viewpoints for object inspection (Trucco et al, 1997)

Fig. 18 Sensor placement graph (Chen & Li, 2004)

In 3D reconstruction and shape processing for reuse of the geometric models by (Doi et al, 2005), a topology which defines the vertex (sampling point) connectivity and the shape of the mesh, is assigned and conserved to meet the desired meshing. Stable meshing, and hence, an accurate approximation, free from the misconnection unavoidable in modeling, is then accomplished.

Fig. 19 The aspect graph of an object (Eggert et al, 1995)

4.7. Active Lighting

Basically, the light position should be determined to achieve adequate illumination, mathematically through the light path, i.e. surface absorption, diffused reflectance, specular reflectance, and image irradiance. Illumination now becomes the most challenging part of system design, and is a major factor when it comes to implementing color inspection (Garcia-Chamizo et al, 2007). Here, when illumination is also considered, the term "sensor" has a border meaning (Quang et al, 2008; Scott, 2009).

Eltoft and deFigueiredo found that illumination control could be used as a means of enhancing image features (Eltoft & deFigueiredo, 1995). Such features are points, edges, and shading patterns, which provide important cues for the interpretation of an image of a scene and the recognition of objects present in it. Based on approximate expressions for the reflectance map of Lambertian and general surfaces, a rigorous discussion on how intensity gradients are dependent on the direction of the light is presented.

Measuring reflection properties of a 3D object is useful for active lighting control. Lensch et al. presented a method to select advantageous measurement directions based on analyzing the estimation of the bi-directional reflectance distribution function (BRDF) (Lensch, Lang, Sa & Seidel, 2003). Ellenrieder et al. derive a phenomenological model of the BRDF of non-Lambertian metallic materials typically used in industrial inspection. They show how the model can be fitted to measured reflectance values and how the fitted model can be used to determine a suitable illumination position. Together with a given sensor pose, this illumination position can be used to calculate the necessary shutter time, aperture, focus setting and expected gray value to successfully perform a given inspection task (Ellenrieder, Wohler & d'Angelo, 2005).

When the reflectance of the scene under analysis is uniform, the intensity profile of the image spot is a Gaussian and its centroid is correctly detected assuming an accurate peak position detector. However, when a change of reflectance occurs on the scene, the intensity profile of the image spot is no longer Gaussian. Khali et al. present two heuristic models to improve the sensor accuracy in the case of a variable surface reflectance (Khali, Savaria, Houle, Rioux, Beraldin & Poussart, 2003).

To better describe the properties, Ikeuchi et al. showed a sensor modeler, VANTAGE, to place the light sources and cameras for object recognition (Ikeuchi & Robert, 1991). It was proposed to solve the detectability of both light sources and cameras. It determined the illumination/observation directions using a tree-structured representation and AND/OR operations. The sensor is defined as consisting of not only the camera, but multiple components, e.g. a photometric stereo. It is represented as a sensor composition tree (SC tree). Finally, the appearance of object surfaces is predicted by applying the SC tree to the object and is followed by the action of sensor planning.

In order to automatically place light sources for maximum visual information recovery, (Vazquez, 2007) defined a metric to calculate the amount of information relative to an object that is effectively communicated to the user given a fixed camera position. This measure is based on an information-based concept, the Shannon entropy, and will be applied to the problem of automatic selection of light positions in order to adequately illuminate an object.

For the surveillance task of a mobile robot in indoor living space, beside the real conditions and poses, it was demonstrated that an illumination model is necessary for a planning behavior and good image quality results (Schroeter et al, 2009). The luminance of an object surface at position (x; y) depends on the observer direction j is modeled as L = f(x; y; j). The update of the illumination model can be done by the use of a sequence of exposures with a standard camera.

To determine the optimal lighting position in view of 3D reconstruction error minimization, Belhaoua et al. proposed an evaluation criterion for each tentative position uses the contrast across object edges and the variance-based edge detection results. The best lighting position corresponds to the minimum variance and the maximum contrast values. Results show that the optimization of the lighting position leads indeed to minimization of the 3D measurement errors. The search procedure for optimal lighting source position is being fully automated using Situation Graph Trees (SGTs) as a planning tool and is included in a complete dynamic re-planning tool for 3D automated vision-based reconstruction tasks (Belhaoua et al, 2009).

Marchand et al. proposed an approach to control camera position and/or lighting conditions in an environment using image gradient information. The goal is to ensure a good viewing condition and good illumination of an object to perform vision-based tasks such as recognition and tracking. Within the visual servoing framework, the solution is to maximize the brightness of the scene and maximize the contrast in the image. They consider arbitrary combinations of either static, moving lights and cameras. The method is independent of the structure, color and aspect of the objects (Marchand, 2007). For examples, illuminating the Venus of Milo is planned as in Fig. 20.

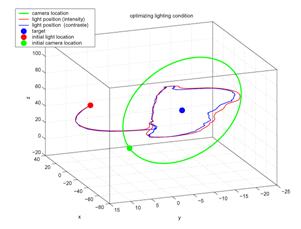
Fig. 20 En example of camera and light source position control (Marchand, 2007)

5. Conclusions and Future Trends

This paper has summarized the recent development of active visual perception strategies in robotic applications. Typical contributions are given for inspection, surveillance, recognition, search, exploration, localization, navigation, manipulation, tracking, mapping, modeling, assembly and disassembly. Representative works are listed for readers to have a general overview of the state-of-the art. A bundle of methods are investigated in regard to solutions of visual perception acquisition problems, including visibility analysis, coverage and occlusion, spatial tessellation, data fusion, geometrical and graphic analysis, cost function evaluation, cooperative network, multi-agent, evolutionary computation, fuzzy inference, neural network, learning and expert system, information entropy, Bayesian reasoning, hypothesis and verification, etc. Issues of gaze, attention, dynamic configuration, and active lighting are also addressed, while they are not emphasized in this survey. The largest volume of literature reviewed is related to inspection and object modeling, which correspond to model-based and non-model based vision tasks. They contribute about 15% and 9% in the number of total publications, respectively.

Now let us look back from today into the survey by (Tarabanis et al, 1995a), where we can find that almost all of the “future directions” pointed out 15 years ago have been studied with considerable advancements. While some typical problems still need to have better solutions, new challenges and requirements are emerging in the field. To make active perception even more effective in practical robotics, the challenges either are currently under investigation in research groups worldwide or need to be solved in the future. The following suggest some trends.

(1) Internet of Things

Internet of Things refers to the networked interconnection of everyday objects whose purpose would be to make all things communicable. Every human being (as well as robot) is surrounded by 1,000 to 5,000 objects. The Internet of Things would encode trillions of objects and follow the movement of those objects. If all objects of daily life can be identified and managed by computers in the same way humans can, the robots would have no difficulty in deciding their actions therefore be able to instantaneously identify any kind of object. Of course, it is impossible to encode all things. Robot vision can be a part of ambient intelligence between the environment and human beings. The visual knowledge obtained by active perception might be combined with other information from the Internet of Things. Therefore, the robot itself should be included in the internet of things and become the most intelligent object.

(2) Data fusion and reliable decision

Today, multiple data sources are often obtained in a robotic system. When more than one kind of video cameras, ranger sensor, sonar, infrared, ultrasound, GPS, Compass, IMU, odometers, etc. are used together, vision perception can be made more reliable by data fusion. Consequently, a consistent representation should be developed so that fusion of positional data, range data, and appearance data can be realized to allow for safe path planning and effective view planning.

(3) Cooperative networks

For a complex vision task in a large scale environment, multiple robots can be adopted to accomplish the goal efficiently. This, however, requires a good scheme of system integration. Real-time data communication among all agents is required for systematic coordination. When exchanging detailed 2D/3D imagery data is impossible, extraction and representation of high-level abstract data should be implemented. Control and decision in such systems will then become a critical issue.

(4) On-site solution of uncertainty

In purposive perception planning for either exploration, navigation, modeling, or other tasks, there is a situation that the robot has to work in a dynamic environment and the perception may associate with noises or uncertainties. Research in this issue has long been active in the field, but it seems that no complete solutions will be available in the near future.

(5) Reconfigurable systems

As autonomous robots are expected to work in complex environments, fixed component structures are not capable of dealing with all situations. Flexible design makes the system reconfigurable during the task execution. Researchers are clearly aware of this issue, but it is a very slow progress to implement such device due to high cost. Beside the hardware mechanism, software for control and recalibration has to be developed concurrently.

(6) Understanding and semantic representation

Relying solely on spatial data, active perception could not be very intelligent. Initially, the scene is seen in terms of a cloud of surface points, which would include millions of points. For scene interpretation, labeling can be processed to mark meaningful structures. Converting from source image data to geometrical shapes makes the scene understandable, and converting from geometrical shapes to semantic representation makes it much more understandable to the robot. By constructing geometrical map and semantic map, knowledge of the spatial relationship about the environment can be used for reasoning to find objects and events. Such high-level representation and reasoning depend on, but also affect, the low-level vision perception.

(7) Application in practical robots

In recent years, although researchers have continued working on the theoretical formulation of active sensor planning, many works tend to combine the existing methods with industrial application such as inspection, recognition, search, modeling, tracking, exploration, assembly and disassembly. Theoretical solutions are rarely perfect in practical engineering applications. Many sophisticated practical techniques have to be developed.

REFERENCES

Abidi,B.R., Aragam,N.R., Yao,Y., & Abidi,M.A. (2008). Survey and Analysis of Multimodal Sensor Planning and Integration for Wide Area Surveillance. ACM Computing Surveys 41(1).

Abrams,S., Allen,P.K., & Tarabanis,K. (1999). Computing camera viewpoints in an active robot work cell. International Journal of Robotics Research 18(3), 267-285.

Al-Hmouz,R., & Challa,S. (2005). Optimal placement for opportunistic cameras using genetic algorithm. Proceedings of the 2005 Intelligent Sensors, Sensor Networks & Information Processing Conference 337-341.

Amin,S., Tanoto,A., Witkowski,U., Ruckert,U., & bdel-Wahab,S. (2008). Modified local navigation strategy for unknown environment exploration. Icinco 2008: Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics, Vol Ra-1 - Robotics and Automation, Vol 1 171-176.

Angella,F., Reithler,L., & Gallesio,F. (2007). Optimal deployment of cameras for video surveillance systems. 2007 IEEE Conference on Advanced Video and Signal Based Surveillance 388-392.

Arman,F., & Aggarwal,J.K. (1993). Model-Based Object Recognition in Dense-Range Images - A Review. Computing Surveys 25(1), 5-43.

Asai,T., Kanbara,M., & Yokoya,N. Data acquiring support system using recommendation degree map for 3D outdoor modeling. Proceedings of the society of photo-optical instrumentation engineers (SPIE). H4910. 2007

Baker,P., & Kamgar-Parsi,B. (2010). Using shorelines for autonomous air vehicle guidance. Computer Vision and Image Understanding, 723-729.

Bakhtari,A., & Benhabib,B. (2007). An active vision system for multitarget surveillance in dynamic environments. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics 37(1), 190-198.

Bakhtari,A., Mackay,M., & Benhabib,B. (2009). Active-Vision for the Autonomous Surveillance of Dynamic, Multi-Object Environments. Journal of Intelligent & Robotic Systems 54(4), 567-593.

Bakhtari,A., Naish,M.D., Eskandari,M., Croft,E.A., & Benhabib,B. (2006). Active-vision-based multisensor surveillance - An implementation. IEEE Transactions on Systems Man and Cybernetics Part C-Applications and Reviews 36(5), 668-680.

Ballesta,M., Gil,A., Reinoso,O., Julia,M., & Jimenez,L. (2010). Multi-robot map alignment in visual SLAM. WSEAS Transactions on Systems 213-222.

Banish,M., Rodgers,M., Hyatt,B., Edmondson,R., Chenault,D., Heym,J., DiNardo,P., Gruber,B., Johnson,J., & Dobson,K. (2010). Exploiting uncalibrated stereo on a UAV platform. Proceedings of the SPIE 76921T.

Banta,J.E., Wong,L.M., Dumont,C., & Abidi,M.A. (2000). A next-best-view system for autonomous 3-D object reconstruction. IEEE Transactions on Systems Man and Cybernetics Part A-Systems and Humans 30(5), 589-598.

Bardon,C., Hodge,L., & Kamel,A. (2004). A framework for optimal multi-agent sensor planning. International Journal of Robotics & Automation 19(3), 152-166.

Barreto,J.P., Perdigoto,L., Caseiro,R., & Araujo,H. (2010). Active Stereo Tracking of N <= 3 Targets Using Line Scan Cameras. IEEE Transactions on Robotics 26(3), 442-457.

Baumann,M., Leonard,S., Croft,E.A., & Little,J.J. (2010). Path Planning for Improved Visibility Using a Probabilistic Road Map. IEEE Transactions on Robotics 26(1), 195-200.

Baumann,M.A., Dupuis,D.C., Leonard,S., Croft,E.A., & Little,J.J. (2008). Occlusion-Free Path Planning with a Probabilistic Roadmap. 2008 IEEE/RSJ International Conference on Robots and Intelligent Systems, Vols 1-3, Conference Proceedings 2151-2156.

Belhaoua,A., Kohler,S., & Hirsch,E. (2009). Determination of Optimal Lighting Position in View of 3D Reconstruction Error Minimization. The 10th European Congress of Stereology and Image Analysis 408-414.

Biegelbauer,G., Vincze,M., & Wohlkinger,W. (2010). Model-based 3D object detection. Machine Vision and Applications 21(4), 497-516.

Bjorkman,M., & Kragic,D. Combination of foveal and peripheral vision for object recognition and pose estimation. IEEE Int. Conf. Robotics and Automation. 5135-5140. 2004.

Blaer,P.S., & Allen,P.K. (2007). Data acquisition and view planning for 3-D modeling tasks. 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vols 1-9 423-428.

Blaer,P.S., & Allen,P.K. (2009). View Planning and Automated Data Acquisition for Three-Dimensional Modeling of Complex Sites. Journal of Field Robotics 26(11-12), 865-891.

Bodor,R., Drenner,A., Schrater,P., & Papanikolopoulos,N. (2007). Optimal camera placement for automated surveillance tasks. Journal of Intelligent & Robotic Systems 50(3), 257-295.

Borenstein,J., Borrell,A., Miller,R., & Thomas,D. (2010). Heuristics-enhanced dead-reckoning (HEDR) for accurate position tracking of tele-operated UGVs. Proceedings of the SPIE 76921R.

Borotschnig,H., & Paletta,L. (2000). Appearance-based active object recognition. Image and Vision Computing 18(9), 715-727.

Borrmann,D., Elseberg,J., Lingemann,K., Nüchter,A., & Hertzberg,J. (2008). Globally consistent 3D mapping with scan matching. Robotics and Autonomous Systems 56(2), 130-142.

Bottino,A., & Laurentini,A. (2006a). What's NEXT? An interactive next best view approach. Pattern Recognition 39(1), 126-132.

Bottino,A., & Laurentini,A. (2008). A nearly optimal sensor placement algorithm for boundary coverage. Pattern Recognition 41(11), 3343-3355.

Bottino,A., & Laurentini,A. (2006b). Experimental results show near-optimality of a sensor location algorithm. 2006 IEEE International Conference on Robotics and Biomimetics, Vols 1-3 340-345.

Bottino,A., Laurentini,A., & Rosano,L. (2007). A tight lower bound for art gallery sensor location algorithms. 12Th IEEE International Conference on Emerging Technologies and Factory Automation, pp. 434-440.

Bottino,A., Laurentini,A., & Rosano,L. (2009). A new lower bound for evaluating the performances of sensor location algorithms. Pattern Recognition Letters 30(13), 1175-1180.

Boutarfa,A., Bouguechal,N.E., & Emptoz,H. (2008). A New Approach for An Automated Inspection System of the Manufactured Parts. International Journal of Robotics & Automation 23(4), 220-226.

Briggs,A.J., & Donald,B.R. (2000). Visibility-based planning of sensor control strategies. Algorithmica 26(3-4), 364-388.

Budiharto,W., Jazidie,A., & Purwanto,D. (2010). Indoor Navigation Using Adaptive Neuro Fuzzy Controller for Servant Robot. Proceedings of the 2010 Second International Conference on Computer Engineering and Applications (ICCEA 2010) 582-586.

Byun,J.E., & Nagata,T. (1996). Active visual sensing of the 3-D pose of a flexible object. Robotica 14 173-188.

Caglioti,V. (2001). An entropic criterion for minimum uncertainty sensing in recognition and localization - Part I: Theoretical and conceptual aspects. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics 31(2), 187-196.

Callari,F.G., & Ferrie,F.P. (2001). Active object recognition: Looking for differences. International Journal of Computer Vision 43(3), 189-204.

Callieri,M., Fasano,A., Impoco,G., Cignoni,P., Scopigno,R., Parrini,G., & Biagini,G. RoboScan: an automatic system for accurate and unattended 3D scanning. 805-812. 2004. 2nd International Symposium on 3D Date Processing.

Carrasco,M., & Mery,D. Automatic multiple visual inspection on non-calibrated image sequence with intermediate classifier block. 371-384. 2007. Advances in Image and Video Technology.

Cassinis,R., & Tampalini,F. (2007). AMIRoLoS an active marker internet-based robot localization system. Robotics and Autonomous Systems 55(4), 306-315.

Chang,M.H., & Park,S.C. (2009). Automated scanning of dental impressions. Computer-Aided Design 41(6), 404-411.

Chang,M.S., Chou,J.H., & Wu,C.M. (2010). Design and Implementation of a Novel Outdoor Road-Cleaning Robot. Advanced Robotics 24(1-2), 85-101.

Chen,F., Brown,G.M., & Song,M.M. (2000). Overview of three-dimensional shape measurement using optical methods. Optical Engineering 39(1), 10-22.

Chen,H.Y., & Li,Y.F. (2009). Dynamic View Planning by Effective Particles for Three-Dimensional Tracking. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics 39(1), 242-253.

Chen,H.Y., & Li,Y.F. (2008). Data fusion for three-dimensional tracking using particle techniques. Optical Engineering 47(1).

Chen,S.H., & Liao,T.T. (2009). An automated IC chip marking inspection system for surface mounted devices on taping machines. Journal of Scientific & Industrial Research 68(5), 361-366.

Chen,S.Y., & Li,Y.F. (2005). Vision sensor planning for 3-D model acquisition. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics 35(5), 894-904.

Chen,S.Y., & Li,Y.F. (2004). Automatic sensor placement for model-based robot vision. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics 34(1), 393-408.

Chen,S.Y., Li,Y.F., & Zhang,J.W. (2008a). Active Sensor Planning for Multiview Vision Tasks. Springer.

Chen,S.Y., Li,Y.F., & Zhang,J.W. (2008b). Vision processing for realtime 3-D data acquisition based on coded structured light. IEEE Transactions on Image Processing 17(2), 167-176.

Chen,X., & Davis,J. (2008). An occlusion metric for selecting robust camera configurations. Machine Vision and Applications 19(4), 217-222.

Chu,G.W., & Chung,M.J. (2002). Autonomous selection and modification of camera configurations using visibility and manipulability measures. Journal of Robotic Systems 19(5), 219-230.

Cohen,O., & Edan,Y. (2008). A sensor fusion framework for online sensor and algorithm selection. Robotics and Autonomous Systems 56(9), 762-776.

Cowan,C.K., & Kovesi,P.D. (1988). Automatic sensor placement from vision task requirements. IEEE Trans.pattern analysis and machine intelligence 407-416.

Craciun,D., Paparoditis,N., & Schmitt,F. (2008). Automatic pyramidal intensity-based laser scan matcher for 3D modeling of large scale unstructured environments. Proceedings of the Fifth Canadian Conference on Computer and Robot Vision 18-25.

Das,S., & Ahuja,N. (1996). Active surface estimation: Integrating coarse-to-fine image acquisition and estimation from multiple cues. Artificial Intelligence 83(2), 241-266.

de Ruiter,H., Mackay,M., & Benhabib,B. (2010). Autonomous three-dimensional tracking for reconfigurable active-vision-based object recognition. Proceedings of the Institution of Mechanical Engineers Part B-Journal of Engineering Manufacture 224(B3), 343-360.

Deinzer,F., Derichs,C., Niemann,H., & Denzler,J. (2009). A Framework for Actively Selecting Viewpoints in Object Recognition. International Journal of Pattern Recognition and Artificial Intelligence 23(4), 765-799.

Dickinson,S.J., Christensen,H.I., Tsotsos,J.K., & Olofsson,G. (1997). Active object recognition integrating attention and viewpoint control. Computer Vision and Image Understanding 67(3), 239-260.

Doi,J., Sato,W., & Miyake,T. Topology conserved 3D reconstruction and shape processing for reuse of the geometric models. IEEE International Conference on Information Reuse and Integration. 410-414. 2005.

Dunn,E., & Olague,G. (2004). Multi-objective sensor planning for efficient and accurate object reconstruction. Applications of Evolutionary Computing 3005 312-321.

Dunn,E., & Olague,G. (2003). Evolutionary computation for sensor planning: The task distribution plan. Eurasip Journal on Applied Signal Processing 2003(8), 748-756.

Dunn,E., Olague,G., & Lutton,E. (2006). Parisian camera placement for vision metrology. Pattern Recognition Letters 27(11), 1209-1219.

Eggert,D., Stark,L., & Bowyer,K. (1995). Aspect Graphs and Their Use in Object Recognition. Annals of Mathematics and Artificial Intelligence 13(3-4), 347-375.

Eidenberger,R., Grundmann,T., Feiten,W., & Zoellner,R. (2008). Fast Parametric Viewpoint Estimation for Active Object Detection. 2008 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems 464-469.

Ellenrieder,M.M., Kruger,L., Stossel,D., & Hanheide,M. (2005). A versatile model-based visibility measure for geometric primitives. Image Analysis (Lecture notes in computer science) 669-678.

Ellenrieder,M.M., Wohler,C., & d'Angelo,P. Reflectivity function based illumination and sensor planning for industrial inspection. 89-98. 2005. Optical Measurement Systems for Industrial Inspection IV (Proceedings of SPIE).

Eltoft,T., & deFigueiredo,R. (1995). Illumination control as a means of enhancing image features in active vision systems. IEEE Trans.Image Processing 4(11), 1520-1530.

Erdem,U.M., & Sclaroff,S. (2006). Automated camera layout to satisfy task-specific and floor plan-specific coverage requirements. Computer Vision and Image Understanding 103(3), 156-169.

Fang,S.F., George,B., & Palakal,M. (2008). Automatic Surface Scanning of 3D Artifacts. Proceedings of the 2008 International Conference on Cyberworlds 335-341.

Farshidi,F., Sirouspour,S., & Kirubarajan,T. (2009). Robust sequential view planning for object recognition using multiple cameras. Image and Vision Computing 27(8), 1072-1082.

Fernandez,P., Rico,J.C., Alvarez,B.J., Valino,G., & Mateos,S. (2008). Laser scan planning based on visibility analysis and space partitioning techniques. International Journal of Advanced Manufacturing Technology 39(7-8), 699-715.

Fiore,L., Somasundaram,G., Drenner,A., & Papanikolopoulos,N. Optimal camera placement with adaptation to dynamic scenes. 956-961. 2008. 2008 IEEE Int. Conf. Robotics and Automation.

Flandin,G., & Chaumette,F. (2001). Vision-based control using probabilistic geometry for objects reconstruction. The 40^th IEEE Conference on Decision and Control. 4152-4157.

Flandin,G., & Chaumette,F. (2002). Visual data fusion for objects localization by active vision. ECCV 312-326.

Frintrop,S., & Jensfelt,P. (2008b). Attentional Landmarks and Active Gaze Control for Visual SLAM. IEEE Transactions on Robotics 24(5), 1054-1065.

Frintrop,S., & Jensfelt,P. (2008a). Active gaze control for attentional visual SLAM. 2008 IEEE International Conference on Robotics and Automation, Vols 1-9 3690-3697.

Gao,J., Gindy,N., & Chen,X. (2006). An automated GD&T inspection system based on non-contact 3D digitization. International Journal of Production Research 44(1), 117-134.

Garcia,H.C., & Villalobos,J.R. (2007b). Automated feature selection methodology for reconfigurable Automated Visual Inspection systems. 2007 IEEE International Conference on Automation Science and Engineering, Vols 1-3 703-708.

Garcia,H.C., & Villalobos,J.R. Development of a methodological framework for the self reconfiguration of automated visual inspection systems. 207-212. 2007a. 2007 5^th IEEE International Conference on industrial Informatics.

Garcia-Chamizo,J.M., Fuster-Guillo,A., & zorin-Lopez,J. (2007). Simulation of automated visual inspection systems for specular surfaces quality control. Advances in Image and Video Technology, Proceedings 4872 749-762.

Gonzalez-Banos,H.H., & Latombe,J.C. (2002). Navigation strategies for exploring indoor environments. International Journal of Robotics Research 21(10-11), 829-848.

Gremban,K.D., & Ikeuchi,K. (1994). Planning Multiple Observations for Object Recognition. International Journal of Computer Vision 12(2-3), 137-172.

Grewe,L., & Kak,A.C. (1995). Interactive Learning of A Multiple-Attribute Hash Table Classifier for Fast Object Recognition. Computer Vision and Image Understanding 61(3), 387-416.

Han,S., Choi,B., & Lee,J. (2008). A precise curved motion planning for a differential driving mobile robot. Mechatronics 18(9), 486-494.

He,B.W., & Li,Y.F. (2006b). A next-best-view method for automatic Modeling of three dimensional objects. Dynamics of Continuous Discrete and Impulsive Systems-Series B-Applications & Algorithms 13E 104-109.

He,B.W., & Li,Y.F. (2006a). A next-best-view method with self-termination in active modeling of 3D objects. 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vols 1-12 5345-5350.

Hernandez,O.J., & Wang,Y.F. (2008). An Autonomous Off-Road Robot Based on Integrative Technologies. 2008 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Vols 1-3 540-545.

Hodge,L., & Kamel,M. (2003). An agent-based approach to multisensor coordination. IEEE Transactions on Systems Man and Cybernetics Part A-Systems and Humans 33(5), 648-662.

Hodge,L., Kamel,M., & Bardon,C. Scalability and optimality in a multi-agent sensor planning system. 74-80. 2004. Soft Computing with Industrial Applications.

Hornung,A., Zeng,B.Y., & Kobbelt,L. (2008). Image selection for improved multi-view stereo. 2008 IEEE Conference on Computer Vision and Pattern Recognition, Vols 1-12 2696-2703.

Hovland,G.E., & McCarragher,B.J. (1999). Control of sensory perception in a mobile navigation problem. International Journal of Robotics Research 18(2), 201-212.

Howarth,R.J. (2005). Spatial models for wide-area visual surveillance: Computational approaches and spatial building-blocks. Artificial Intelligence Review 23(2), 97-154.

Huang,Y.B., & Qian,X. (2008a). An efficient sensing localization algorithm for free-form surface digitization. Journal of Computing and Information Science in Engineering 8(2).

Huang,Y.B., & Qian,X.P. (2007). A dynamic sensing-and modeling approach to three-dimensional point- and area-sensor integration. Journal of Manufacturing Science and Engineering-Transactions of the Asme 129(3), 623-635.

Huang,Y.B., & Qian,X.P. (2008b). An efficient sensing localization algorithm for free-form surface digitization. 27Th Computers and Information in Engineering Conference, Vol 2, Pts A and B 2007 - Proceedings of the Asme International Design Engineering Technical Conferences and Computers and Information in Engineering Conference 327-336.

Hubner,W., & Mallot,H.A. (2007). Metric embedding of view-graphs - A vision and odometry-based approach to cognitive mapping. Autonomous Robots 23(3), 183-196.

Ikeuchi,K., & Robert,J.C. (1991). Modeling Sensor Detectability with the Vantage Geometric Sensor Modeler. IEEE Transactions on Robotics and Automation 7(6), 771-784.

Impoco,G., Cignoni,P., & Scopigno,R. (2004). Closing gaps by clustering unseen directions. Proceedings of the International Conference on Shape Modeling and Applications 307-+.

Jang,H.Y., Moradi,H., Le Minh,P., Lee,S., & Han,J. (2008). Visibility-based spatial reasoning for object manipulation in cluttered environments. Computer-Aided Design 40(4), 422-438.

Jang,H.Y., Moradi,H., Lee,S., Jang,D., Kim,E., & Han,J. (2007). A graphics hardware-based accessibility analysis for real-time robotic manipulation. Dynamics of Continuous Discrete and Impulsive Systems-Series B-Applications & Algorithms 14 97-106.

Janoos,F., Machiraju,R., Parent,R., Davis,J.W., & Murray,A. Sensor configuration for coverage optimization for surveillance applications. 49105. 2007. Proceedings of the society of photo-optical instrumentation engineers (SPIE).

Jonnalagadda,K., Lumia,R., Starr,G., & Wood,J. Viewpoint selection for object reconstruction using only local geometric features. IEEE International Conference on Robotics and Automation. 2116-2122. 2003.

Kaess,M., & Dellaert,F. (2010). Probabilistic structure matching for visual SLAM with a multi-camera rig. Computer Vision and Image Understanding 286-296.

Kaminka,G.A., Schechter-Glick,R., & Sadov,V. (2008). Using sensor morphology for multirobot formations. IEEE Transactions on Robotics 24(2), 271-282.

Kang,F., Li,J.J., & Xu,Q. (2008). Virus coevolution partheno-genetic algorithms for optimal sensor placement. Advanced Engineering Informatics 22(3), 362-370.

Kececi,F., et al. Improving visually servoed disassembly operations by automatic camera placement. IEEE Int.Conf.on Robotics and Automation, 2947-2952. 1998.

Khali,H., Savaria,Y., Houle,J.L., Rioux,M., Beraldin,J.A., & Poussart,D. (2003). Improvement of sensor accuracy in the case of a variable surface reflectance gradient for active laser range finders. IEEE Transactions on Instrumentation and Measurement 52(6), 1799-1808.

Kim,M.Y., & Cho,H.S. An active view planning method for mobile robots using a trinocular visual sensor. 74-83. 2003. Optomechatronic Systems IV (Proceedings of SPIE).

Kollar,T., & Roy,N. (2008). Trajectory optimization using reinforcement, learning for map exploration. International Journal of Robotics Research 27(2), 175-196.

Kwok, N.M. and Rad, A.B. (2006). A modified particle filter for simultaneous localization and mapping, Journal of Intelligent and Robotic Systems, 46(4), 365-382.

Kristensen,S. (1997). Sensor planning with Bayesian decision theory. Robotics and Autonomous Systems 19(3), 273-286.

Krotkov,E., & Bajcsy,R. (1993). Active Vision for Reliable Ranging - Cooperating Focus, Stereo, and Vergence. International Journal of Computer Vision 11(2), 187-203.

Kumar,A. (2008). Computer-vision-based fabric defect detection: A survey. IEEE Transactions on Industrial Electronics 55(1), 348-363.

Kuno,Y., Okamoto,Y., & Okada,S. (1991). Robot Vision Using A Feature Search Strategy Generated from A 3-D Object Model. IEEE Transactions on Pattern Analysis and Machine Intelligence 13(10), 1085-1097.

Kutulakos,K.N., & Dyer,C.R. (1994). Recovering Shape by Purposive Viewpoint Adjustment. International Journal of Computer Vision 12(2-3), 113-136.

Kutulakos,K.N., & Dyer,C.R. (1995). Global Surface Reconstruction by Purposive Control of Observer Motion. Artificial Intelligence 78(1-2), 147-177.

Lang,J., & Jenkin,M.R.M. (2000). Active object modeling with VIRTUE. Autonomous Robots 8(2), 141-159.

Larsson,S., & Kjellander,J.A.P. (2008). Path planning for laser scanning with an industrial robot. Robotics and Autonomous Systems 56(7), 615-624.

Lensch,H.P.A., Lang,J., Sa,A.M., & Seidel,H.P. (2003). Planned sampling of spatially varying BRDFs. Computer Graphics Forum 22(3), 473-482.

Li,X.K., & Wee,W.G. (2008). Sensor error modeling and compensation for range images captured by a 3D ranging system. Measurement Science & Technology 19(12).

Li,Y.D., & Gu,P.H. (2004). Free-form surface inspection techniques state of the art review. Computer-Aided Design 36(13), 1395-1417.

Li,Y.F., He,B., & Bao,P. (2005). Automatic view planning with self-termination in 3D object reconstructions. Sensors and Actuators A-Physical 122(2), 335-344.

Li,Y.F., He,B., Chen,S., & Bao,P. (2005). A view planning method incorporating self-termination for automated surface measurement. Measurement Science & Technology 16(9), 1865-1877.

Li,Y.F., & Liu,Z.G. (2005). Information entropy-based viewpoint planning for 3-D object reconstruction. IEEE Transactions on Robotics 21(3), 324-337.

Li,Y.F., & Liu,Z.G. (2003). Method for determining the probing points for efficient measurement and reconstruction of freeform surfaces. Measurement Science & Technology 14(8), 1280-1288.

Liang,C., & Wong,K.Y.K. (2010). 3D reconstruction using silhouettes from unordered viewpoints. Image and Vision Computing 28(4), 579-589.

Lim,S.N., Davis,L., & Mittal,A. Task scheduling in large camera networks. 397-407. 2007. COMPUTER VISION - ACCV.

Lim,S.N., Davis,L.S., & Mittal,A. (2006). Constructing task visibility intervals for video surveillance. Multimedia Systems 12(3), 211-226.

Lin,H.Y., Liang,S.C., & Wu,J.R. 3D shape recovery with registration assisted stereo matching. 596-603. 2007. Pattern Recognition and Image Analysis (Lecture notes in computer science).

Liu,M., Liu,Y.S., & Ramani,K. (2009). Computing global visibility maps for regions on the boundaries of polyhedra using Minkowski sums. Computer-Aided Design 41(9), 668-680.

Liu,M., & Ramani,K. (2009). On minimal orthographic view covers for polyhedra. Smi 2009: IEEE International Conference on Shape Modeling and Applications, Proceedings 96-102.

Liu,Y.H. (2009). Replicator Dynamics in the Iterative Process for Accurate Range Image Matching. International Journal of Computer Vision 83(1), 30-56.

Liu,Y.S., & Heidrich,W. (2003). Interactive 3D model acquisition and registration. 11Th Pacific Conference on Computer Graphics and Applications, Proceedings 115-122.

Loniot,B., Seulin,R., Gorria,P., & Meriaudeau,F. Simulation for an automation of 3D acquisition and post-processing. 35604. 2007. Eight International Conference on Quality Control by Artificial Vision.

Ma,C.Y.T., Yau,D.K.Y., Chin,J.C., Rao,N.S.V., & Shankar,M. (2009). Matching and Fairness in Threat-Based Mobile Sensor Coverage. IEEE Transactions on Mobile Computing 8(12), 1649-1662.

Mackay,M., & Benhabib,B. (2008a). A Multi-Camera Active-Vision System for Dynamic Form Recognition. Innovations and Advanced Techniques in Systems, Computing Sciences and Software Engineering 26-31.

Mackay,M., & Benhabib,B. Active-vision system reconfigutration for form recognition in the presence of dynamic obstacles. 188-207. 2008b. Articulated Motion and Deformable Objects.

MacKinnon,D., Aitken,V., & Blais,F. (2008a). Adaptive laser range scanning. 2008 American Control Conference, Vols 1-12 3857-3862.

MacKinnon,D., Aitken,V., & Blais,F. (2008b). Review of measurement quality metrics for range imaging. Journal of Electronic Imaging 17(3).

Madhuri,P., Nagesh,A.S., Thirumalaikumar,M., Varghese,Z., & Varun,A.V. (2009). Performance analysis of smart camera based distributed control flow logic for machine vision applications. 2009 IEEE International Conference on Industrial Technology, Vols 1-3 90-95.

Marchand,E. (2007). Control camera and light source positions using image gradient information. IEEE international conference on robotics and automation 417-422.

Marchand,E., & Chaumette,F. (1999a). Active vision for complete scene reconstruction and exploration. IEEE Transactions on Pattern Analysis and Machine Intelligence 21(1), 65-72.

Marchand,E., & Chaumette,F. (1999b). An autonomous active vision system for complete and accurate 3D scene reconstruction. International Journal of Computer Vision 32(3), 171-194.

Martinez,S.S., Ortega,J.G., Garcia,J.G., & Garcia,A.S. An expert knowledge based sensor planning system for car headlight lens inspection. 1123-1128. 2008. Computational Intelligence in Decision and Control.

Martinez,S.S., Ortega,J.G., Garcia,J.G., & Garcia,A.S. (2009). A sensor planning system for automated headlamp lens inspection. Expert Systems with Applications 36(5), 8768-8777.

Martins,F.A.R., Garcia-Bermejo,J.G., Casanova,E.Z., & Gonzalez,J.R.P. (2005). Automated 3D surface scanning based on CAD model. Mechatronics 15(7), 837-857.

Martins,F.A.R., Garcia-Bermejo,J.G., Zalama,E., & Peran,J.R. (2003). An optimized strategy for automatic optical scanning of objects in reverse engineering. Journal of Engineering Manufacture 217(8), 1167-1171.

Maruyama,K., Takase,R., Kawai,Y., Yoshimi,T., Takahashi,H., & Tomita,F. (2010). Semi-Automated Excavation System for Partially Buried Objects Using Stereo Vision-Based Three-Dimensional Localization. Advanced Robotics 24(5-6), 651-670.

Mason,S. (1997). Heuristic reasoning strategy for automated sensor placement. Photogrammetric Engineering and Remote Sensing 63(9), 1093-1102.

Mitsunaga,N., & Asada,M. (2006). How a mobile robot selects landmarks to make a decision based on an information criterion. Autonomous Robots 21(1), 3-14.

Mittal,A. (2006). Generalized multi-sensor planning. ECCV 3951 522-535.

Mittal,A., & Davis,L.S. Visibility analysis and sensor planning in dynamic environments. 175-189. 2004. COMPUTER VISION - ECCV.

Mittal,A., & Davis,L.S. (2008). A general method for sensor planning in multi-sensor systems: Extension to random occlusion. International Journal of Computer Vision 76(1), 31-52.

Miura,J., & Ikeuchi,K. (1998). Task-oriented generation of visual sensing strategies in assembly tasks. IEEE Transactions on Pattern Analysis and Machine Intelligence 20(2), 126-138.

Mostofi,Y., & Sen,P. (2009). Compressive Cooperative Sensing and Mapping in Mobile Networks. 2009 American Control Conference, Vols 1-9 3397-3404.

Motai,Y., & Kosaka,A. (2008). Hand-Eye Calibration Applied to Viewpoint Selection for Robotic Vision. IEEE Transactions on Industrial Electronics 55(10), 3731-3741.

Murrieta-Cid,R., Muoz,L., & Alencastre,M. Maintaining Visibility of a Moving Holonomic Target at a Fixed Distance with a Non-Holonomic Robot. IEEE/RSJ Int.Conf.on Intelligent Robots and Systems (IROS) . 2005.

Nabbe,B., & Hebert,M. (2007). Extending the path-planning horizon. International Journal of Robotics Research 26(10), 997-1024.

Naish,M.D., Croft,E.A., & Benhabib,B. (2003). Coordinated dispatching of proximity sensors for the surveillance of manoeuvring targets. Robotics and Computer-Integrated Manufacturing 19(3), 283-299.

Nayak,J., Gonzalez-Argueta,L., Song,B., Roy-Chowdhury,A., & Tuncel,E. (2008). Multi-Target Tracking Through Opportunistic Camera Control in A Resource Constrained Multimodal Sensor Network. 2008 Second ACM/IEEE International Conference on Distributed Smart Cameras 77-86.

Nelson,B.J., & Papanikolopoulos,N.P. (1996). Robotic visual servoing and robotic assembly tasks. IEEE Robotics and automation magazine 23-31.

Newman,T.S., & Jain,A.K. (1995). A Survey of Automated Visual Inspection. Computer Vision and Image Understanding 61(2), 231-262.

Nickels,K., DiCicco,M., Bajracharya,M., & Backes,P. (2010). Vision guided manipulation for planetary robotics - position control. Robotics and Autonomous Systems 121-129.

Nikolaidis,S., Ueda,R., Hayashi,A., & Arai,T. (2009). Optimal Camera Placement Considering Mobile Robot Trajectory. 2008 IEEE International Conference on Robotics and Biomimetics, Vols 1-4 1393-1396.

Nilsson,U., Ogren,P., & Thunberg,J. (2008). Optimal Positioning of Surveillance UGVs. 2008 IEEE/RSJ International Conference on Robots and Intelligent Systems, Vols 1-3, Conference Proceedings 2539-2544.

Nilsson,U., Ogren,P., & Thunberg,J. Towards Optimal Positioning of Surveillance UGVs. 8th International Conference on Cooperative Control and Optimization , 221-233. 2009. 8th International Conference on Cooperative Control and Optimization.

Nüchter,A., & Hertzberg,J. (2008). Towards semantic maps for mobile robots. Robotics and Autonomous Systems 56(11), 915-926.

Null,B.D., & Sinzinger,E.D. Next best view algorithms for interior and exterior model acquisition. 668-677. 2006. Advances in Visual Computing.
Olague,G. (2002). Automated photogrammetric network design using genetic algorithms. Photogrammetric Engineering and Remote Sensing 68(5), 423-431.

Olague,G., & Dunn,E. (2007). Development of a practical photogrammetric network design using evolutionary computing. Photogrammetric Record 22(117), 22-38.

Olague,G., & Mohr,R. (2002). Optimal camera placement for accurate reconstruction. Pattern Recognition 35(4), 927-944.

Oniga,F., & Nedevschi,S. (2010). Processing Dense Stereo Data Using Elevation Maps: Road Surface, Traffic Isle, and Obstacle Detection. IEEE Transactions on Vehicular Technology 59(3), 1172-1182.

Park,T.H., Kim,H.J., & Kim,N. (2006). Path planning of automated optical inspection machines for PCB assembly systems. International Journal of Control Automation and Systems 4(1), 96-104.

Perng,D.B., Chen,S.H., & Chang,Y.S. (2010). A novel internal thread defect auto-inspection system. International Journal of Advanced Manufacturing Technology 47(5-8), 731-743.

Pito,R. (1999). A solution to the next best view problem for automated surface acquisition. IEEE Transactions on Pattern Analysis and Machine Intelligence 21(10), 1016-1030.

Popescu,V., Sacks,E., & Bahmutov,G. (2004). Interactive modeling from dense colour and sparse depth. 2Nd International Symposium on 3D Data Processing, Visualization, and Transmission, Proceedings 430-437.

Prieto,F., Lepage,R., Boulanger,P., & Redarce,T. (2003). A CAD-based 3D data acquisition strategy for inspection. Machine Vision and Applications 15(2), 76-91.

Prieto,F., Redarce,T., Boulanger,P., & Lepage,R. (2001). Tolerance control with high resolution 3D measurements. Third International Conference on 3-D Digital Imaging and Modeling, Proceedings 339-346.

Prieto,F., Redarce,T., Lepage,R., & Boulanger,P. (2002). An automated inspection system. International Journal of Advanced Manufacturing Technology 19(12), 917-925.

Quang,L.B., Kim,D., & Lee,S. (2008). Auto-focusing Technique in a Projector-Camera System. 2008 10Th International Conference on Control Automation Robotics & Vision: Icarv 2008, Vols 1-4 1914-1919.

Radovnikovich,M., Vempaty,P., & Cheok,K. (2010). Auto-Preview Camera Orientation for Environment Perception on a Mobile Robot. Proceedings of the SPIE - The International Society for Optical Engineering 75390Q.

Rae,A., & Basir,O. (2009). Reducing Multipath Effects in Vehicle Localization by Fusing GPS with Machine Vision. 12Th International Conference on Information Fusion 2099-2106.

Raviv,D., & Herman,M. (1994). A Unified Approach to Camera Fixation and Vision-Based Road Following. IEEE Transactions on Systems Man and Cybernetics 24(8), 1125-1141.

Reddi,S., & Loizou,G. (1995). Analysis of Camera Behavior During Tracking. IEEE Transactions on Pattern Analysis and Machine Intelligence 17(8), 765-778.

Reed,M.K., & Allen,P.K. (2000). Constraint-based sensor planning for scene modeling. IEEE Transactions on Pattern Analysis and Machine Intelligence 22(12), 1460-1467.

Riggs,T., Inanc,T., & Weizhong,Z. (2010). An Autonomous Mobile Robotics Testbed: Construction, Validation, and Experiments. IEEE Transactions on Control Systems Technology 757-766.

Rivera-Rios,A.H., Shih,F.L., & Marefat,M. Stereo camera pose determination with error reduction and tolerance satisfaction for dimensional measurements. IEEE International Conference on Robotics and Automation (ICRA). 423-428. 2005.

Roy,S.D., Chaudhury,S., & Banerjee,S. (2000). Isolated 3-d object recognition through next view planning. IEEE Transactions on Systems Man and Cybernetics Part A-Systems and Humans 30(1), 67-76.

Roy,S.D., Chaudhury,S., & Banerjee,S. (2004). Active recognition through next view planning: a survey. Pattern Recognition 37(3), 429-446.

Roy,S.D., Chaudhury,S., & Banerjee,S. (2005). Recognizing large isolated 3-D objects through next view planning using inner camera invariants. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics 35(2), 282-292.

Royer,E., Lhuillier,M., Dhome,M., & Lavest,J.M. (2007). Monocular vision for mobile robot localization and autonomous navigation. International Journal of Computer Vision 74(3), 237-260.

Saadatseresht,M., Samadzadegan,F., & Azizi,A. (2005). Automatic camera placement in vision metrology based on a fuzzy inference system. Photogrammetric Engineering and Remote Sensing 71(12), 1375-1385.

Saadatseresht,M., & Varshosaz,M. (2007). Visibility prediction based on artificial neural networks used in automatic network design. Photogrammetric Record 22(120), 336-355.

Sablatnig,R., Tosovic,S., & Kampel,M. Next view planning for a combination of passive and active acquisition techniques. 62-69. 2003. Fourth International Conference on 3-D Digital Imaging and Modeling.

Sakane,S., Kuruma,T., Omata,T., & Sato,T. (1995). Planning Focus of Attention for Multifingered Hand with Consideration of Time-Varying Aspects. Computer Vision and Image Understanding 61(3), 445-453.

Schroeter,C., Hoechemer,M., Mueller,S., & Gross,H.M. Autonomous Robot Cameraman - Observation Pose Optimization for a Mobile Service Robot in Indoor Living Space. 2199-2204. 2009. IEEE International Conference on Robotics and Automation-ICRA.

Scott,W.R. (2009). Model-based view planning. Machine Vision and Applications 20(1), 47-69.

Scott,W.R., Roth,G., & Rivest,J.F. (2003). View planning for automated three-dimensional object reconstruction and inspection. Acm Computing Surveys 35(1), 64-96.

Se,S., & Jasiobedzki,P. (2007). Stereo-vision based 3D modeling for unmanned ground vehicles. Unmanned Systems Technology IX - Proceedings of SPIE X5610.

Sebastian,J.M., Garcia,D., Traslosheros,A., Sanchez,F.M., & Dominguez,S. A new automatic planning of inspection of 3D industrial parts by means of visual system. 1148-1159. 2007. Image Analysis and Recognition (Lecture notes in computer science).

Seo,Y.W., & Urmson,C. (2008). A Perception Mechanism for Supporting Autonomous Intersection Handling in Urban Driving. 2008 IEEE/RSJ International Conference on Robots and Intelligent Systems, Vols 1-3, Conference Proceedings 1830-1835.

Sheng,W.H., Xi,N., Song,M., & Chen,Y.F. (2001a). CAD-guided robot motion planning. Industrial Robot 28(2), 143-151.

Sheng,W.H., Xi,N., Song,M.M., & Chen,Y.F. (2003). CAD-guided sensor planning for dimensional inspection in automotive manufacturing. IEEE-ASME Transactions on Mechatronics 8(3), 372-380.

Sheng,W.H., Xi,N., Song,M.M., & Chen,Y.F. (2001b). Graph-based surface merging in CAD-guided dimensional inspection of automotive parts. 2001 IEEE International Conference on Robotics and Automation, Vols I-Iv, Proceedings 3127-3132.

Shi,Q., Xi,N., & Zhang,C. (2010). Develop a Robot-Aided Area Sensing System for 3D Shape Inspection. Journal of Manufacturing Science and Engineering-Transactions of the Asme 132(1).

Shih,C.S., & Gerhardt,L.A. (2006). Integration of view planning with nonuniform surface sampling techniques for three-dimensional object inspection. Optical Engineering 45(11).

Shimizu,S., Yamamoto,K., Wang,C.H., Satoh,Y., Tanahashi,H., & Niwa,Y. (2005). Detection of moving object by mobile Stereo Omnidirectional System (SOS). Electrical Engineering in Japan 152(3), 29-38.

Shinzato,P., Fernandes,L., Osorio,F., & Wolf,D. (2010). Path Recognition for Outdoor Navigation Using Artificial Neural Networks: Case Study. 2010 IEEE International Conference on Industrial Technology (ICIT 2010) 1457-1462.

Shubina,K., & Tsotsos,J.K. (2010). Visual search for an object in a 3D environment using a mobile robot. Computer Vision and Image Understanding 114(5), 535-547.

Shum,H.Y., Hebert,M., Ikeuchi,K., & Reddy,R. (1997). An integral approach to free-form object modeling. IEEE Transactions on Pattern Analysis and Machine Intelligence 19(12), 1366-1370.

Sivaram,G.S.V.S., Kankanhalli,M.S., & Ramakrishnan,K.R. (2009). Design of Multimedia Surveillance Systems. Acm Transactions on Multimedia Computing Communications and Applications 5(3).

Stemmer,A., Schreiber,G., Arbter,K., & Albu-Schaffer,A. Robust Assembly of Complex Shaped Planar Parts Using Vision and Force. IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems. 493-500. 2006.

Sujan,V.A., & Dubowsky,S. (2005a). Efficient information-based visual robotic mapping in unstructured environments. International Journal of Robotics Research 24(4), 275-293.

Sujan,V.A., & Dubowsky,S. (2005b). Visually guided cooperative robot actions based on information quality. Autonomous Robots 19(1), 89-110.

Sujan,V.A., & Meggiolaro,M.A. (2005). Intelligent and efficient strategy for unstructured environment sensing using mobile robot agents. Journal of Intelligent & Robotic Systems 43(2-4), 217-253.

Sun,C., Wang,P., Tao,L., & Chen,S. (2008). Method of scanning-path determination for color three-dimensional laser measurement. Optical Engineering 47(1).

Sun,J., Sun,Q., & Surgenor,B.W. (2007). Adaptive visual inspection for assembly line parts verification. Wcecs 2007: World Congress on Engineering and Computer Science 575-580.

Sun,T.H., Tseng,C.C., & Chen,M.S. (2010). Electric contacts inspection using machine vision. Image and Vision Computing 28(6), 890-901.

Suppa,M., & Hirzinger,G. (2007). Multisensory exploration of Robot workspaces. Tm-Technisches Messen 74(3), 139-146.

Sutton,M.A., & Stark,L. (2008). Function-based reasoning for goal-oriented image segmentation. Towards Affordance-Based Robot Control 4760 159-172.

SyedaMahmood,T.F. (1997). Data and model-driven selection using color regions. International Journal of Computer Vision 21(1-2), 9-36.

Tarabanis,K., Tsai,R.Y., & Allen,P.K. (1994). Analytical Characterization of the Feature Detectability Constraints of Resolution, Focus, and Field-Of-View for Vision Sensor Planning. Cvgip-Image Understanding 59(3), 340-358.

Tarabanis,K., Tsai,R.Y., & Kaul,A. (1996). Computing occlusion-free viewpoints. IEEE Transactions on Pattern Analysis and Machine Intelligence 18(3), 279-292.

Tarabanis,K.A., Allen,P.K., & Tsai,R.Y. (1995a). A Survey of Sensor Planning in Computer Vision. IEEE Transactions on Robotics and Automation 11(1), 86-104.

Tarabanis,K.A., Tsai,R.Y., & Allen,P.K. (1995b). The Mvp Sensor Planning System for Robotic Vision Tasks. IEEE Transactions on Robotics and Automation 11(1), 72-85.

Taylor,C.J., & Spletzer,J. A bounded uncertainty approach to cooperative localization using relative bearing constraints. 2506-2512. 2007. 2007 IEEE/RSJ INTERNATIONAL CONFERENCE ON INTELLIGENT ROBOTS AND SYSTEMS.

Thielemann,J., Breivik,G., & Berge,A. (2010). Robot navigation and obstacle detection in pipelines using time-of-flight imagery. Proceedings of the SPIE - The International Society for Optical Engineering 75260O.

Thomas,U., Molkenstruck,S., Iser,R., & Wahl,F.M. Multi Sensor Fusion in Robot Assembly Using Particle Filters. ICRA. 3837-3843. 2007.

Torres-Mendez,L.A., & Dudek,G. (2008). Inter-image statistics for 3D environment modeling. International Journal of Computer Vision 79(2), 137-158.

Treuillet,S., Albouy,B., & Lucas,Y. (2009). Three-Dimensional Assessment of Skin Wounds Using a Standard Digital Camera. IEEE Transactions on Medical Imaging 28(5), 752-762.

Treuillet,S., Albouy,B., & Lucas,Y. (2007). Finding two optimal positions of a hand-held camera for the best reconstruction. 2007 3Dtv Conference 173-176.

Triebel,R., & Burgard,W. Recovering the shape of objects in 3D point clouds with partial occlusions. 13-22. 2008. Field and Service Robotics: Results of the 6^th International Conference.

Trucco,E., Umasuthan,M., Wallace,A.M., & Roberto,V. (1997). Model-based planning of optimal sensor placements for inspection. IEEE Transactions on Robotics and Automation 13(2), 182-194.

Tsai,T.H., & Fan,K.C. (2007). An image matching algorithm for variable mesh surfaces. Measurement 40(3), 329-337.

Ulvklo,M., Nygards,J., Karlholm,J., & Skoglar,P. Image processing and sensor management for autonomous UAV surveillance. 50-65. 2004. Airborne Intelligence (Proceedings of SPIE).

Vazquez,P.P. (2007). Automatic light source placement for maximum visual information recovery. Computer Graphics Forum 26(2), 143-156.

Wang,P., Zhang,Z.M., & Sun,C.K. (2009). Framework for adaptive three-dimensional acquisition using structured light vision system. Journal of Vacuum Science & Technology B 27(3), 1418-1421.

Wang,P.P., & Gupta,K. (2007). View planning for exploration via maximal C-space entropy reduction for robot mounted range sensors. Advanced Robotics 21(7), 771-792.

Wang,P.P., & Gupta,K. (2006). A configuration space view of view planning. 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vols 1-12 1291-1297.

Wang,P.P., Krishnamurti,R., & Gupta,K. View planning problem with combined view and traveling cost. 711-716. 2007. IEEE international conference on robotics and automation.

Wang,Y., Hussein,I.I., & Erwin,R.S. Awareness-based decision making for search and tracking. 3169-3175. 2008. 2008 American Control Conference.

Wenhardt,S., Deutsch,B., Angelopoulou,E., & Niemann,H. (2007). Active visual object reconstruction using D-, E-, and T-Optimal next best views. 2007 IEEE Conference on Computer Vision and Pattern Recognition, Vols 1-8 2810-2816.

Whaite,P., & Ferrie,F.P. (1997). Autonomous exploration: Driven by uncertainty. IEEE Transactions on Pattern Analysis and Machine Intelligence 19(3), 193-205.

Wheeler,M.D., & Ikeuchi,K. (1995). Sensor Modeling, Probabilistic Hypothesis Generation, and Robust Localization for Object Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence 17(3), 252-265.

Wong,C., & Kamel,M. Comparing viewpoint evaluation functions for model-based inspectional coverage. 287-294. 2004. 1^st Canadian Conference on Computer and Robot Vision.

Wu,P., Suzuki,H., & Kase,K. (2005). Model-based simulation system for planning numerical controlled multi-axis 3D surface scanning machine. Jsme International Journal Series C-Mechanical Systems Machine Elements and Manufacturing 48(4), 748-756.

Yang,C.C., & Ciarallo,F.W. (2001). Optimized sensor placement for active visual inspection. Journal of Robotic Systems 18(1), 1-15.

Yao,Y., Chen,C.H., Abidi,B., Page,D., Koschan,A., & Abidi,M. (2010). Can You See Me Now? Sensor Positioning for Automated and Persistent Surveillance. IEEE Transactions on Systems Man and Cybernetics Part B-Cybernetics 40(1), 101-115.

Ye,Y.M., & Tsotsos,J.K. (1999). Sensor planning for 3D object search. Computer Vision and Image Understanding 73(2), 145-168.

Yegnanarayanan,V., Umamaheswari,G.K., & Lakshmi,R.J. (2009). On A Graph Theory Based Approach For Improved Computer Vision. Proceedings of the 2009 International Conference on Signal Processing Systems 660-664.

Zavidovique,B., & Reynaud,R. (2007). The situated vision: a concept to facilitate the autonomy of the systems. Traitement du Signal 24(5), 309-322.

Zetu,D., & Akgunduz,A. (2005). Shape recovery and viewpoint planning for reverse engineering. International Journal of Advanced Manufacturing Technology 26(11-12), 1370-1378.

Zhang,G., Ferrari,S., & Qian,M. (2009). An Information Roadmap Method for Robotic Sensor Path Planning. Journal of Intelligent & Robotic Systems 56(1-2), 69-98.

Zhang,Z.G., Peng,X., Shi,W.Q., & Hu,X.T. (2000). A survey of surface reconstruction from multiple range images. Systems Integrity and Maintenance, Proceedings 519-523.

Zhou,H., & Sakane,S. Learning Bayesian network structure from environment and sensor planning for mobile robot localization. IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems. 76-81. 2003.

Zhou,X.L., He,B.W., & Li,Y.F. (2008). A New View Planning Method for Automatic Modeling of Three Dimensional Objects. Intelligent Robotics and Applications, Pt I, Proceedings 5314 161-170.

Zingaretti,P., & Frontoni,E. (2006). Appearance based robotics. IEEE Robotics & Automation Magazine 13(1), 59-68.

Zussman,E., Schuler,H., & Seliger,G. (1994). Analysis of the Geometrical Features Detectability Constraints for Laser-Scanner Sensor Planning. International Journal of Advanced Manufacturing Technology 9(1), 56-64.

The International Journal of Robotics Research

This work was supported by NSFC (60870002), ZJNSF(R1110679), and RGC-HK (CityU 117507)

Vol. x, No. y, December 2011, pp. a–b

DOI: 10.1177/0278364xxx

Figures appear in color online: http://ijr.sagepub.com